Vi begynner med å merke oss at formelen for luftmotstand, \(F_d\) er gitt i polare koordinater. Når vi sjekker posisjonen vår med instrumentene om bord på romskipet, får vi kartesiske koordinater tilbake. La oss begynne med å utlede posisjon og hastighet fra kartesiske koordinater til polare. Vi starter med å definere enhetsvektorene, \(\hat{\textbf{e}}_r\) og \(\hat{\textbf{e}}_\theta\). Siden vi til enhver tid kommer til å befinne oss langs planetens ekvator, vil komponenten i z-retning alltid være 0. Vi får:
\(\begin{align} \hat{\textbf{e}}_r&=r\,\cos\big(\theta(t)\big)\hat{\textbf{x}}+r\,\sin\big(\theta(t)\big)\hat{\textbf{y}}\\ \hat{\textbf{e}}_\theta&=-r\,\sin\big(\theta(t)\big)\hat{\textbf{x}}+r\,\cos\big(\theta(t)\big)\hat{\textbf{y}} \end{align}\)
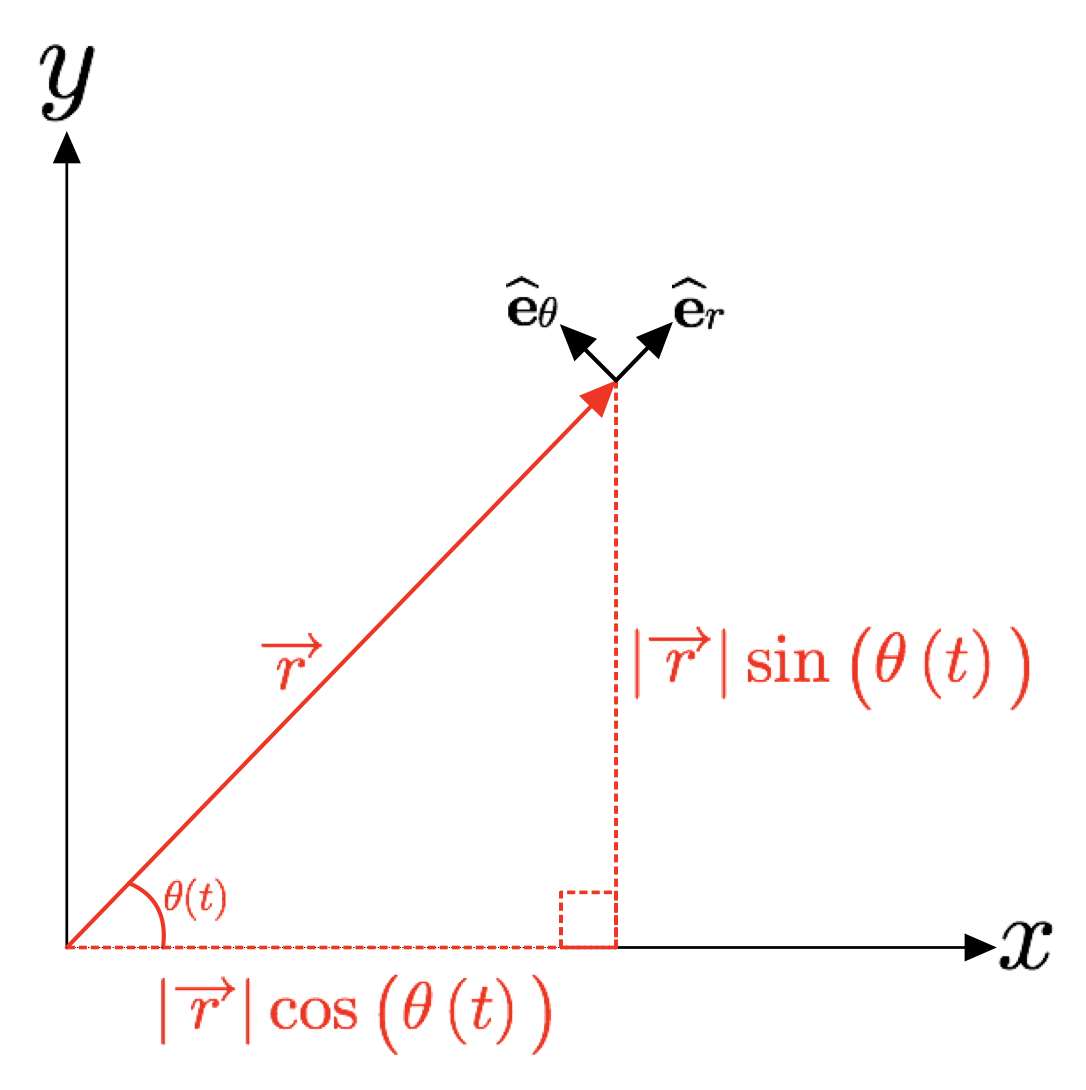
Dere kan sjekke at dette stemmer ved å bruke Pythagoras' læresetning. Vi kan også sjekke hva som skjer om vi deriverer disse enhetsvektorene med hensyn på tid. Merk at vi her må bruke kjerneregel. Vi får
\(\begin{align} \frac{d\,\hat{\textbf{e}}_r}{dt}&=-r\,\sin\big(\theta(t)\big)\cdot\frac{d\theta(t)}{dt}\hat{\textbf{x}}+r\cos\big(\theta(t)\big)\cdot\frac{d\theta(t)}{dt}\hat{\textbf{y}}\\ &=\omega(t)\cdot\hat{\textbf{e}}_\theta\\ \frac{d\,\hat{\textbf{e}}_\theta}{dt}&=-r\,\cos\big(\theta(t)\big)\cdot\frac{d\theta(t)}{dt}\hat{\textbf{x}}-r\,\sin\big(\theta(t)\big)\cdot\frac{d\theta(t)}{dt}\hat{\textbf{y}}\\ &=-\omega(t)\cdot\hat{\textbf{e}}_r \end{align}\)
Husk at den deriverte av \(\theta(t)\) er vinkelfarten, \(\omega(t)\). Vi har heller ingen y-komponent i hastigheten vår. Hvordan kan vi finne hastighetsvektoren i polare koordinater? Jo, vi deriverer posisjonsvektoren! Vi lar \(x\) og \(y\) være komponentene til posisjonen i kartesiske koordinater, og \(v_x\) og \(v_y\) være komponentene til hastigheten i kartesiske koordinater. Husk at posisjonsvektoren i polare koordinater ser slik ut:
\(\vec{r}=r\,\hat{\textbf{e}}_r\)
hvor \(r=|r|=\sqrt{x(t)^2+y(t)^2}\). Vinkelen \(\theta(t)\) er gitt ved \(\arctan\Big(\frac{y(t)}{x(t)}\Big)\). Sjekk selv, om du ser hvorfor i Figur 1.
Vi deriverer posisjonsvektoren for å finne hastighetsvektor. Her må vi bruke produktregel og kjerneregel flere ganger. Vi starter med radiell komponent, \(r=\sqrt{x(t)^2+y(t)^2}\).
\(\begin{align} v_r=\frac{d\,r}{dt}&=\frac{d}{dt}\bigg(\sqrt{x(t)^2+y(t)^2}\bigg)\\ &=\frac{1}{2\sqrt{x(t)^2+y(t)^2}}\cdot\Big(2x(t)x'(t)+2y(t)y'(t)\Big)\\ &=\frac{x(t)\,v_x(t)+y(t)\,v_y(t)}{\sqrt{x(t)^2+y(t)^2}} \end{align}\)
For å finne \(\theta\)-komponenten, må vi derivere \(\arctan\Big(\frac{y(t)}{x(t)}\Big)\). Heldigvis er det ikke så vanskelig, for vi har at \(\arctan'(x)=\frac{1}{1+x^2}\). Vi får da, for tangentiell komponent:
\(\begin{align} v_\theta=r\frac{d\,\theta(t)}{dt}&=r\frac{d}{dt}\Bigg(\arctan\bigg(\frac{y(t)}{x(t)}\bigg)\Bigg)\\ &=r\frac{1}{1+\Big(\frac{y(t)}{x(t)}\Big)^2}\cdot\Bigg(\frac{y'(t)x(t)-y(t)x'(t)}{\big(x(t)\big)^2}\Bigg)\\ &=r\frac{x(t)\,v_y(t)-y(t)\,v_x(t)}{\big(x(t)\big)^2+\big(y(t)\big)^2} \end{align}\)
Dette ble pene utrykk. Nei, da. Men det er sånn det blir. Vi bruker disse formlene for å gjøre om fra kartesisk til polare koordinater. Vi går også andre veien, men det kommer vi ikke til å ta med her. Det skal være "grei" skuring å finne ut av det på egen hånd, så dere er velkomne til å prøve selv.
Vi starter klokka og tar tiden. Dette er planen vår:
| Tid (s) | Handling |
|---|---|
| 0 | Brems romskipet med 20 %. |
| 450 | Slipp løs landingsfartøyet med 1/4 av hastigheten romskipet har. |
| 2500 | Åpne fallskjermen. |
Dette er verdiene vi kommer til å bruke:
| Romskip | Landingsfartøy | Fallskjerm | |
|---|---|---|---|
| Areal (m2) | 16.0 | 0.3 | 70 |
| Masse (kg) | 1100.0 | 90.0 | - |
Vi har antatt at massen til landingsfartøyet inkluderer fallskjermens masse.
Det er noen grenser vi vet vi må forholde oss til. Nemlig at verken romskipet eller landingsfartøyet tåler et krafttrykk på over 107 Pa (Pascal: kg/m3). Fallskjermen tåler heller ikke krefter på over 250 kN. Dessuten vet vi at grensen for å få til en soft landing er 3.0 m/s i radiell retning. Vi plotter derfor verdier for dette og mer, slik at vi kan ha full kontroll over alt som skjer. Dette er resultatet:
Boosted with dv= [1809394.87540424 0. ] at time t= 0 s.
Lander launched with dv= 0.25*vel= [-60.58733923 99.20488693] m/s at t= 450 s.
Opened parachute at t= 2500 s at height 40147 m. Ground hit after 14512.786450127312 s.
Soft landing performed, with final radial velocity v_r=-2.784942675738035 m/s.
Her er plottet av selve landingen:
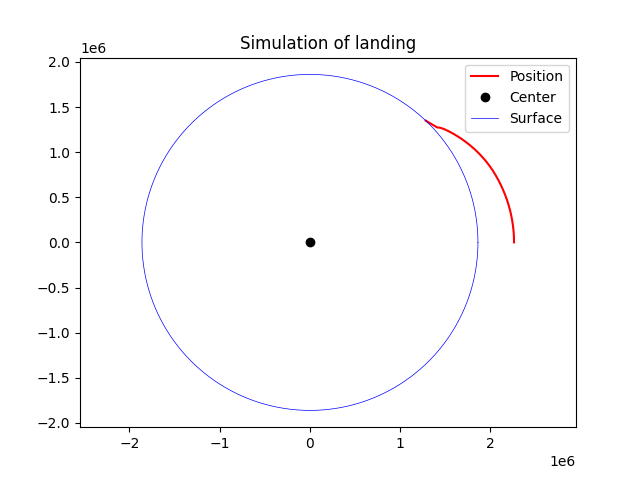
Som dere ser, mister vi høyde når vi bremser. Vi har også plottet det slik at massen endres når vi velger å skyte ut landingsfartøyet. Altså vet vi ikke hva som skjer videre med romskipet.
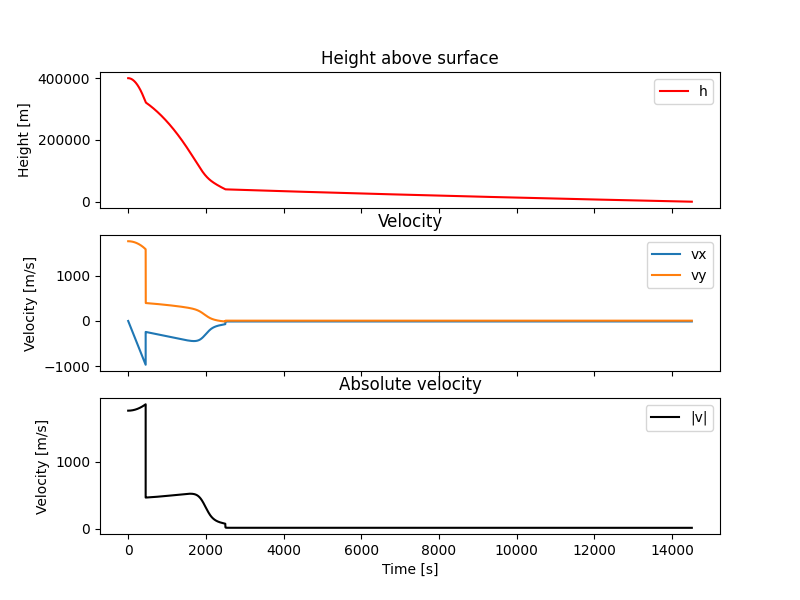
Vi kan se på Figur 3 når de ulike handlingene ble utført, og hva de gjorde med hastigheten. Det er vanskelig å se hva som skjer med hastigheten mot slutten av ferden, så vi kan se på et plott av bare radiell hastighetskomponent.
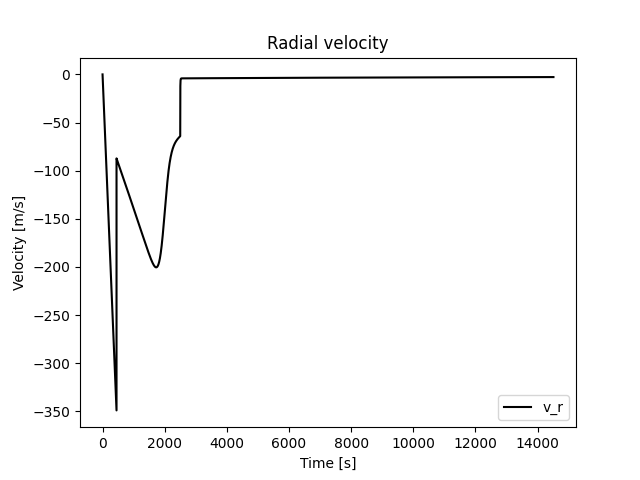
Her også ser vi hva som skjer med \(v_r\) ved de ulike handlingene. Vi har lagt inn tester i programmet vårt som forteller oss om vi har for stor hastighet når vi lander. Som dere kunne se i stad, hadde vi en hastighet på under 3 m/s, så vi klarte en soft landing.
Så til kreftene og trykket. Det kan være vanskelig å lese av plottet hvilke verdier det blir, men vi har også her lagt inn tester for de ulike grensene.
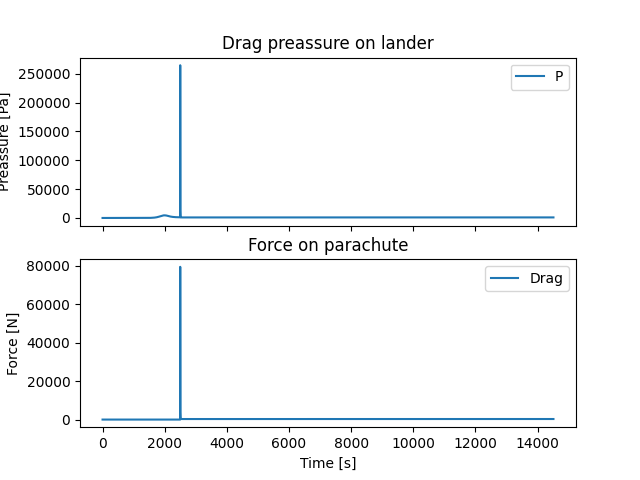
Vi ser tydelig at trykket aldri blir større enn grensen på 107 Pa, og at kreftene på fallskjermen aldri blir større enn 250 kN. Dette lover godt! Nå er det på tide å teste på ekte. Vi stiller inn kameraet og filmer alt som skjer. I tillegg får vi beskjeder på instrumentbordet vårt om noe skulle gå galt.
En liten ting. Husker dere at vi ønsket å lande på et gitt sted? Det kan vi begynne med å si at vi ikke kommer til å få til. Da vi gjorde de utregningene tok vi ikke hensyn til at romskipet ikke tålte å falle evig rundt planeten. Da vi prøvde å la romskipet falle til det tidspunktet vi hadde målinger for, ble friksjonskreftene på romskipet alt for store. Vi har likevel valgt å ha med verdier for hvor landingsstedet vi hadde ønsket å lande på vil være i det vi lander, og avstanden til det.
Dette er resultatene vi får:
Time: 0 s, spacecraft boosted with delta-v (-0, -1764.67, -0) m/s.
Landing module launched at time 450 s with delta-v (-258.257, 98.1683, 0) m/s.
Parachute with area 70 m^2 deployed at time 1200 s.
Successfully landed on planet 6 at time 1560.72 s with velocity 2.79098 m/s.
Dere ser også at vi måtte gjøre noen små endringer. Dette er litt prøv-og-feil, men vi klarte det! Vil dere se video av hele sulamitten? Vil dere? Ja? Greit, her er den:

Dere kan følge hele ferden som den er beskrevet over. Det første som skjer er at romskipet bremser. Dette gjør at tyngdekraften begynner å trekke det ned mot planeten. Det neste som skjer er at landingsfartøyet blir skutt ut. Det faller fortere og fortere ned mot bakken, før fallskjermen blir skutt ut og vi daler trygt ned på bakken.
Nå skal vi se på hvordan simuleringen vår gikk i forhold til det faktiske resultatet. Vi starter med boosten. Vi beregnet at boosten skulle være
[1809394.87540424 0. ],
mens den faktisk var
[0 -1764.0]
Her er det noe rart som har skjedd. Det kan se ut som at det er en faktor 103 som er feil, som kan komme av feil i konvertering mellom meter og kilometer. At boosten faktisk var i y-retning og ikke i x-retning handler mest sannsynlig om at da vi gjorde simuleringen har vi transponert vektoren, slik at vektoren ser slikt ut
\(\begin{align} \begin{bmatrix} x\\ y \end{bmatrix} \end{align}\),
i stedet for slik ut
\(\begin{align} \begin{bmatrix} x&y \end{bmatrix} \end{align}\).
Dette gjør vi om slik at vi kan ha snudd i feil rekkefølge. I praksis har det ikke så veldig mye å si, annet enn at vi har modellert en ferd oppover mot nordpolen i stedet for langs ekvator. Minustegnet kommer av at da vi simulerte, ville en prosentfaktor av hastighetsvektoren gi en ending i hastighet, mens når vi faktisk bremser må vi bestemme om det er en økning eller senkning av hastigheten. Den relative feilen er veldig stor, så det er ikke noe poeng i å regne den ut. Lurer du på hva relativ feil er? Hvis du ikke husker det skal vi friske opp minnet ditt.
Først starter vi med absolutt feil. Dette er den tallmessige feilen. For eksempel hvis du skal koke ris og trenger 150 gram. Du føler deg selvsikker og prøver å beregne så nøyaktig du kan mens du heller risen i en skål. Deretter måler du hvor mye ris det faktisk er i skålen. La oss si du har vært kokk i mange år, og dermed har litt erfaring. Du veier risen og ser at du har 147 gram i skålen. Den absolutte feilen er da
\(|147-150|=3\).
Du bommet med 3 gram, som ikke er så mye. Gratulerer. Grunnen til at vi bruker absoluttegn er fordi vi kan få negative tall. Vi er kun interesserte i størrelsen til tallet, ikke noe mer. Men hva sier dette tallet deg egentlig? Du fikk en feil på 3 gram. Det er lite dersom du skal ha 10 kg, men det er mye hvis du skal ha 5 gram. Det er her relativ feil kommer inn.
Relativ feil er gitt som absolutt feil delt på størrelsen av det du har forventet. Vi kan regne ut den relative feilen du målte slik:
\(\begin{align} \frac{|147-150|}{|150|}=\frac{3}{150}=0.02 \end{align}\)
Dette viser at feilen din var på 2%. Relativ feil brukes altså når du ønsker å se hva feilen var i forhold til et ønsket utfall.
Det neste vi ser på er boosten vi gir landingsfartøyet i det vi skyter det ut fra romskipet. Vi fikk
[-60.58733923 99.20488693],
mens det faktisk var
(-258.257, 98.1683, 0).
Her er det nok tydelig en feil i x-retning. Vi får en relativ feil på
\(\begin{align} \frac{|-60.587-(-258.257)|}{|-258.257|}=\frac{197.670}{258.257}\approx0.765 \end{align}\).
Altså en ganske stor feil, på 76.5%. Men i y-retning ser vi at tallene er mer like. Vi får
\(\begin{align} \frac{|99.205-98.168|}{|98.168|}=\frac{1.037}{98.168}\approx0.011 \end{align}\),
altså en feil på 1.1%.
Så til selve tidspunktet for landingen. Vi beregnet at vi skulle lande ved tiden
14512.786450127312 s,
mens vi faktisk landet ved tiden
1560.72 s.
Det gir en relativ feil på
\(\begin{align} \frac{|14512.786-1560.720|}{|1560.720|}=\frac{12952.066}{1560.720}\approx8.299 \end{align}\),
som er en feil på 829.9% (!). Heldigvis har dette en logisk forklaring. I innlegget om modellering av atmosfæren lagde vi oss et worst case scenario. Vi lagde en veldig tynn atmosfære, som da strekker seg langt over overflaten til planeten. Dessuten gjør tettheten at den ikke bremser oss særlig mye. Med denne modellen kunne vi anslå at vi ville klare å lande i en tettere atmosfære også.
Helt til slutt skal vi se på den relative feilen i radiell hastighet ved landing. Vi fikk
-2.784942675738035 m/s
fra simuleringen, mens i virkeligheten hadde vi
2.79098 m/s.
Minustegnet er for at radiell hastighet er positiv for bevegelse utover fra planeten, mens fra instrumentene våre får vi absolutt hastighet. Vi sløyfer derfor minustegnet fra vår måling. Den relative feilen her blir
\(\begin{align} \frac{|2.78494-2.79098|}{|2.79098|}=\frac{|-0.006|}{2.79098}\approx0.002 \end{align}\).
Dette gir en feil på 0.2%, som er ganske lite. Vi hadde nok litt flaks ettersom at vi ikke hadde modellen av atmosfæren helt rett, men at vi da likevel lander trygt med en så liten feil er vi meget fornøyde med.
Så til det (for oss) litt kjedelige. Landingsplassen vi hadde sett oss ut. Som forklart tidligere, tok vi avgjørelsen om hvilket sted vi skulle lande da vi hadde svevd rundt planeten en stund. Det, i tillegg til at atmosfæremodellen vår var feil, gjorde at vi ikke hadde sjans til å kunne prøve å lande der vi faktisk ville. Men vi tar det med her likevel. Vi landet på koordinatene
\(\Big(R_p\,,\,\frac{\pi}{2}\,,\,\frac{7.1\pi}{180}\Big)\).
De utregnede koordinatene til landingspunktet vårt var
\(\Big(R_p\,,\,\frac{\pi}{2}\,,\,\frac{67.8\pi}{180}\Big)\).
Vi kan regne ut den faktiske avstanden mellom disse to punktene ved hjelp av formelen for radianer. Den ser slik ut:
\(\begin{align} v_\text{rad}=\frac{b}{r} \end{align}\),
hvor \(v_\text{rad}\) er vinkelen i radianer, \(b\) er buelengden og \(r\) er radiusen. Vi løser for buelengden, som i vårt tilfelle vil gi oss den faktiske avstanden vi bommet med.
\(\begin{align} b&=r\cdot v_\text{rad}\\ &=R_p\cdot\bigg(\frac{67.8\pi-7.1\pi}{180}\bigg)\\ &=1861.7\,km\,\cdot1.1\\ &=2047.9\,km \end{align}\)
Så det var en skikkelig bom. Det tilsvarer nesten å sikte på Oslo, men lande i Roma (2008 km). Heldigvis er det fint i Roma!
Med dette er vår romferd ferdig. Vi har lagd en rakett, skutt den opp og reist til en annen verden. Det neste temaet er relativitetsteori. Det blir kjempespennende! Takk for turen til våre avstigende gjester. Neste stopp: Tideromhaugen. Arrivederci!