Kategorisering av stjerna vår
Vi begynner med et diagram. Nei, ikke et sektordiagram og heller ikke et søylediagram. Dette er et Hertzsprung-Russell-diagram (HR-diagram).
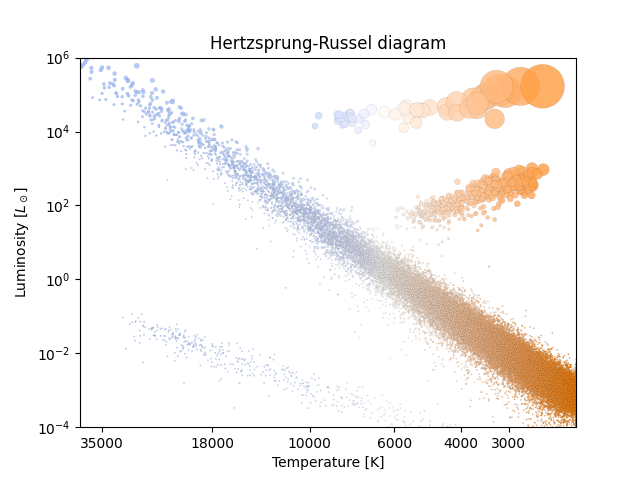
Dette vakre diagrammet kategoriserer stjernene i universet. Den tykke stripa i midten kalles hovedserien. Når en stjerne fødes fra en såkalt giant molecular cloud (GMC, enorm molekylsky), har den veldig lav temperatur, som regel 10-100 Kelvin. Da befinner den seg langt mot høyre i HR-diagrammet. I figur 1 kan dere se at vi har prøvd å gi stjernene størrelser som representerer den faktiske størrelsen deres. Øverst til høyre finnes de røde kjempene. De er ganske "kalde" og har en høy luminositet. Nederst til venstre finnes de hvite dvergene (beklager, det heter ikke kortvokststjerne). Disse er svært varme, men lyser svakt. Dette kommer vi mer tilbake til senere.
Vi begynner med å se på stjerna vår. Først og fremst må vi kategorisere den. Vi starter med å angi luminositeten. Husker du ikke hva luminositet er? Kjapp repetisjon:
Fluks er total mottatt energi per areal per tid. Luminositet er total mottatt energi per tid. Luminositet er altså fluksen summert over hele arealet.
Vi har også Stefan-Boltzmanns lov (SB), \(F=\sigma T^4\), hvor \(\sigma\) er Stefan-Boltzmanns konstant (\(5.67\cdot10^{-8}\,\text{Wm}^{-2}\text{K}^{-4}\)) og \(T\) er overflatetemperaturen til det sorte legeme (legeme som ikke reflekterer noe lys). Her antar vi at stjerna vår er et sort legeme.
Fra dette ser vi at ved å gange opp fluksen fra SB, får vi luminositeten til stjerna. Det gir oss
\(\begin{align} L=F\cdot A=\sigma T^44\pi R^2 \end{align}\)
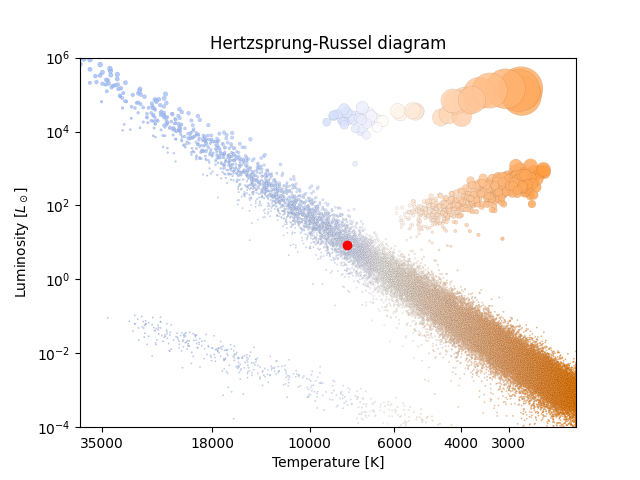
Stjerna vår har radius \(1.06\cdot10^9\,\text{m}\) og temperatur \(7985\,\text{K}\) som gir \(L=3.25\cdot10^{27}\,\text{W}\). Som dere ser på y-aksen i HR-diagrammet, må vi finne luminositeten i forhold til sola sin. Den har luminositet lik \(3.828\cdot10^{26}\,\text{W}\). Dermed får vi at stjerna vår har
\(\begin{align} L=\frac{L}{L_\odot}=8.49\,L_\odot \end{align}\)
Husk at tegnet \(\odot\) betyr sola. Dermed kan vi plotte inn vår kjære stjerne i HR-diagrammet. Den legger seg pent til rette midt i hovedserien. Lurer dere på hvor sola deres ligger? Prøv å finn det ut selv ved hjelp av at solas temperatur er på \(5778\,\text{K}\).
Levetid på hovedserien
Et viktig konsept i astronomien er proporsjonaliteter. Noen av dere har kanskje hørt læreren deres si at tyngdekrafta er proporsjonal, eller "går som" én over radien i andre.
\(F_G=G\frac{mM}{r^2}\)
Her er \(G\) gravitasjonskonstanten (\(6.67\cdot10^{-11}\,\text{m}^3\text{kg}^{-1}\text{s}^{-2}\)) og m-ene er massene. Det vi ser her er at \(G\) og massene er konstanter. Altså tall med en fast verdi. Det eneste som varierer er \(r\), som er avstanden fra objektets sentrum. Hvis vi samler alle konstantene i ett symbol, \(\kappa\), så ser vi at tyngdekrafta kan skrives som
\(F_G=\kappa\frac{1}{r^2}\)
Dersom vi kun ser på variabelen \(r\), og dropper konstanten, får vi proporsjonaliteten. Da kan vi skrive at
\(F_G\propto\frac{1}{r^2}\)
Dette er altså tyngdekrafta, en konstant nær. Det kan hjelpe oss med å se for oss hvordan tyngdekrafta avtar som funksjon av avstanden fra sentrum.
Vi skal benytte følgende proporsjonalitet for å anslå stjerna vår sin tid på hovedserien.
\(t_\text{life}\propto\frac{1}{M^3}\)
Hvor \(M\) er massen til stjerna. Det neste steget er å finne en kjent størrelse som vi kan sammenlikne med. Det mest nærliggende er å bruke sola. Dere har gjort en god jobb, og funnet ut av at sola kommer til å leve på hovedserien i \(\sim10^{10}\) år. Det vil si at forholdet
\(\begin{align} \frac{t_\text{life}}{t_\odot^\text{ms}}=\bigg(\frac{M_\odot}{M}\bigg)^3 \end{align}\)
kan brukes til å finne tiden stjerna vår lever på hovedserien. Her står \(\text{ms}\) for main sequence. Vi skriver om formelen og angir stjerna vår i enhet solmasser. Dermed får vi at stjerna vår antas å leve omtrent \(1.5\cdot10^9\) år, eller én og en halv milliarder år.
La oss presentere to nye proporsjonaliteter.
\(\begin{align} \begin{split} L\propto M^4 \end{split} \quad\quad\quad \begin{split} M\propto T_\text{eff}^2 \end{split} \end{align}\)
Luminositeten er proporsjonal med massen i fjerde potens, og massen er proporsjonal med den effektive temperaturen i andre potens. På samme måte som før bruker vi sola til å finne verdiene. Dersom svaret vi får avviker for mye fra det vi har funnet tidligere, kan vi slå fast at stjerna vår ikke vil være en "veloppdragen" hovedseriestjerne. Resultatene vi får er et avvik på \(72.1\,\%\) i luminositeten og \(2.3\,\%\) i massen. Det vil si at stjerna vår dessverre nok vil være en ganske uregjerlig stjerne.
Giant molecular cloud
Stjerner formes fra noe som kaller kjempestore molekylskyer (GMC). Disse skyene består i hovedsak av hydrogen(H), men også av andre stoffer og støv. Under de rette betingelsene kan skyen kollapse under sin egen gravitasjon, og dette vil føre til at kjernereaksjoner starter. En stjerne er født.
Vår stjerne startet som en GMC. Her har vi antatt følgende.
- Stjerna startet som en sfærisk symmetrisk GMC
- Gasskyen har en temperatur på \(10\,\text{K}\)
- Skyen består av \(75\,\%\) hydrogen og \(25\,\%\) helium (He)
- Skyen kollapser av seg selv, uten ytre påvirkning
- Massen til gasskyen tilsvarer massen til stjerna
Det finnes en formel for den nedre grensen for radien til en GMC, oppkalt etter den engelske astronomen James Jeans (Englands svar på Harry Hole?). Den kalles Jeansradien, og er gitt ved
\(\begin{align} R_J=\sqrt{\frac{15\,k\,T}{4\pi G\mu\,m_H\rho}} \end{align}\)
hvor \(k\) er Boltzmanns konstant (\(1.38\cdot10^{-23}\text{m}^2\text{kg s}^{-2}\text{K}^{-1}\)), \(G\) er gravitasjonskonstanten, \(\mu\,m_H\) er midlere molekylvekt målt i hydrogenmasse og \(\rho\) er tettheten. Siden vi antar at massen til gasskyen er lik massen til stjerna, finner vi tettheten ved \(\rho=\frac{3M}{4\pi R^3}\). For å finne den nedre grensen, løser vi \(R>R_J\). Først opphøyer vi likningen i andre potens. Det vi finner er en øvre grense for radien. Dette skjer fordi vi antar konstant masse. Vi finner følgende.
\(R_\text{max}=\frac{GM\mu m_H}{5kT}=1.1\cdot10^{12}\text{km}\)
La oss anta at radien var \(80\,\%\) av denne. Vi regner ut luminositeten målt i sol-luminositet, og plotter den inn i HR-diagrammet.
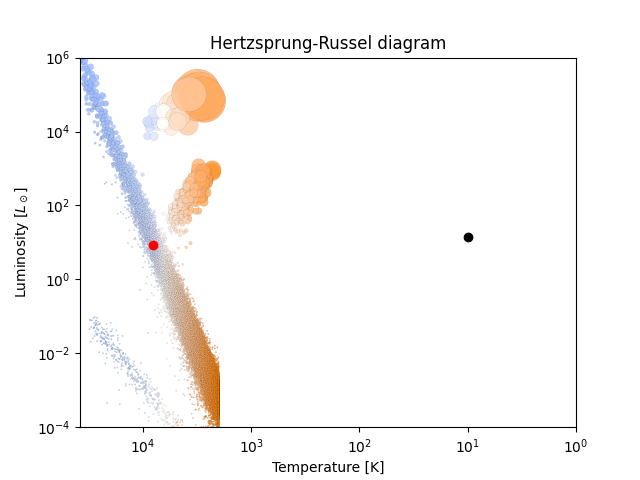
Som dere ser så var luminositeten omtrent den samme da stjerna vår bare bar en gassky. Temperaturen var såpass lav at den plasserer seg godt til høyre for stjernene.
I neste innlegg skal vi se på kjernereaksjonene som skjer i stjerna.
