Kjernetemperatur
Vi starter rett på! Her er antagelsene våre:
- Tettheten til stjerna er uniform, altså likt fordelt utover hele stjerna
- Vi antar ideell gass inne i stjerna, og ser bort fra strålingstrykk når vi bruker trykkloven for ideell gass
- Stjerna er i hydrostatisk likevekt
- Stjerna inneholder kun protoner
Her må vi forklare litt. Dere husker kanskje hva en ideell gass er? Trykk her for å lese om dette. Trykkloven for ideell gass er
\(\begin{align} P=\frac{\rho kT}{\mu m_H} \end{align}\)
hvor \(\rho\) er tettheten til gassen, \(T\) er temperaturen og \(\mu m_H\) er midlere molekylvekt angitt i hydrogenmasse. Midlere molekylvekt regnes ut slik:
\(\begin{align} \mu=\sum_{i=1}^Nf_i\frac{m_i}{m_H} \end{align}\)
Her er \(f_i\) fraksjonsdelen, og \(m_i\) massen av stoff \(i\).
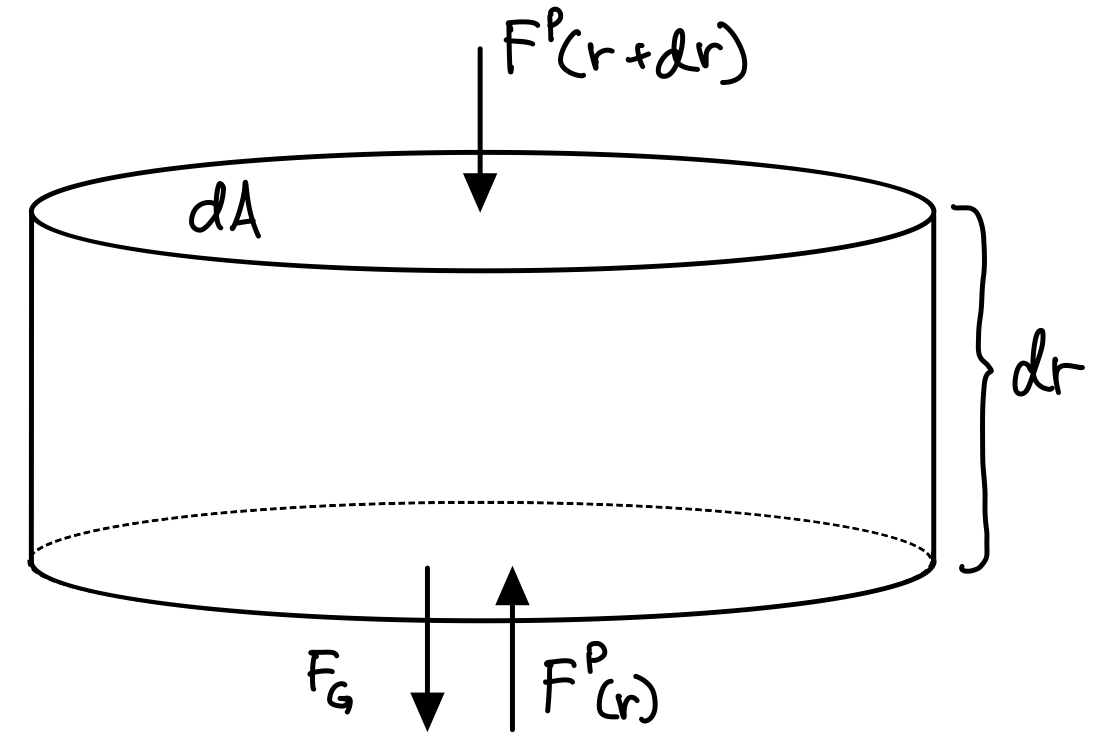
Hydrostatisk likevekt er det som gjør at atmosfæren på jorda ikke faller ned i hodet deres. Formelen for hydrostatisk likevekt ser slik ut:
\(\begin{align} \frac{dP}{dr}=-\rho(r)g(r) \end{align}\)
Siden tettheten er uniform, kan vi sette \(\rho(r)=\rho_0\). Når det gjelder \(g(r)\) så er dette den tyngdeakselerasjonen som virker på et lite delvolum en avstand \(r\) fra sentrum av stjerna. For å finne et uttrykk for denne, trenger vi først å finne et uttrykk for massen til stjerna på innsiden av \(r\). Vi vet at tettheten er gitt ved \(\rho_0=\frac{M}{V}\), hvor \(M\) er massen og \(V=\frac{4}{3}\pi R^3\) er volumet av stjerna. For å finne ut av hva massen innenfor et avgrenset område i stjerna er, så lar vi volumet \(V(r)\) være bestemt av \(r\), og løser likningen for \(M(r)\).
\(\begin{align} M(r)=\frac{4}{3}\rho_0\pi\,r^3 \end{align}\)
Dermed kan vi uttrykke \(g(r)\) slik:
\(\begin{align} g(r)=G\frac{M(r)}{r^2}=\frac{4}{3}G\rho_0\pi\,r \end{align}\)
Her er \(G\) gravitasjonskonstanten (\(6.67\cdot10^{-11}\text{m}^3\text{kg}^{-1}\text{s}^{-2}\)).
Med disse uttrykkene kan vi finne et uttrykk for temperaturendring som funksjon av avstanden fra stjernas sentrum. Ved å derivere den ideelle gassloven får vi
\(\begin{align} \frac{dP}{dr}=\frac{d}{dr}\bigg(\frac{\rho_0k\,T(r)}{\mu m_H}\bigg)=\frac{dT(r)}{dr}\cdot\frac{\rho_0k}{\mu m_H} \end{align}\)
Dette uttrykket må være likt uttrykket for hydrostatisk likevekt. Vi setter dem like hverandre, og løser for temperaturendringen. Det gir oss
\(\begin{align} \frac{dT(r)}{dr}=-\frac{4\pi}{3}G\rho_0\frac{\mu m_H}{k}r \end{align}\)
For å få et uttrykk for kjernetemperaturen \(T_c\), integrerer vi uttrykket fra 0 til radiusen til stjerna, \(R\).
\(\begin{align} \int_0^R\frac{dT}{dr}&=\int_0^R-\frac{4\pi}{3}G\rho_0\frac{\mu m_H}{k}r\,dr\\ T(R)-T(0)&=--\frac{2\pi}{3}G\rho_0\frac{\mu m_H}{k}R^2\\ T_c=T(0)&=T(R)+\frac{2\pi}{3}G\rho_0\frac{\mu m_H}{k}R^2 \end{align}\)
Temperaturen ved overflaten, \(T(R)\) har vi funnet tidligere til å være \(7.99\cdot10^3\text{K}\). Dermed finner vi at kjernetemperaturen er \(1.49\cdot10^7\text{K}\).
Luminositet og energi
Nok en gang begynner vi med noen antagelser.
- Alle kjernereaksjoner finner sted innenfor \(0.2R\)
- Energiproduksjonen kommer fra proton-proton-kjeden og CNO-syklusen
- Kjernen består av \(74.5\%\) hydrogen (H), \(25.3\%\) helium (He) og en samlet andel for karbon (C), nitrogen (N) og oksygen (O) på \(0.2\%\).
Proton-proton-kjeden (pp-chain) er en reaksjon der stjerna omgjøre hydrogen til helium. Denne omdannelsen er mest effektiv ved temperaturer på 15 millioner Kelvin. Kjeden ser slik ut:
\(\begin{align} \varepsilon_\text{pp}\approx\varepsilon_{0,\text{pp}}X_H^2\rho T_6^4 \end{align}\)
Her er \(\varepsilon_{0,\text{pp}}=1.08\cdot10^{-12}\text{Wm}^3\text{kg}^{-2}\) en konstant. \(X_H\) er andelen av hydrogen, \(\rho\) er tettheten og \(T_6\) er temperatur målt i millioner Kelvin.
CNO-syklusen er en annen reaksjon stjerna kan bruke for å omgjøre hydrogen til helium. Temperaturer på ~20 millioner Kelvin er mest effektiv her. Syklusen skrives som følger.
\(\begin{align} \varepsilon_\text{CNO}=\varepsilon_{0,\text{CNO}}X_HX_{CNO}\rho T_6^{20} \end{align}\)
Her er \(\varepsilon_{0,\text{CNO}}=8.24\cdot10^{-31}\text{Wm}^3\text{kg}^{-2}\). \(X_\text{CNO}\) er den samlede andelen karbon, nitrogen og oksygen.
Fra antagelsene våre har vi at
\(X_H=74.5\%=0.074\\ X_\text{CNO}=0.2\%=0.002\)
Symbolet \(\varepsilon\) angir frigitt energi per masse per tid. Siden luminositet er frigitt energi per tid, kan vi skrive
\(\frac{dL}{dm}=\varepsilon\)
Hvis vi ser på en liten sfærisk delmasse med radius \(r\), vil denne massen kunne skrives som \(dm=dV\rho(r)\). Siden tettheten er konstant kan vi skrive \(dm=4\pi r^2\rho_o\,dr\). Dermed får vi dette uttrykket for luminositeten:
\(\begin{align} \frac{dL}{dr}=4\pi r^2\rho_0(\varepsilon_\text{pp}+\varepsilon_\text{CNO}) \end{align}\)
Fra antagelsen vår skjer det kun kjernereaksjoner innenfor en radius på \(0.2R\), så vi integrerer fra 0 til \(0.2R\).
\(\begin{align} \int_0^{0.2R}\frac{dL}{dr}&=\int_0^{0.2R}4\pi r^2\rho_0(\varepsilon_\text{pp}+\varepsilon_\text{CNO})dr\\ L&=\frac{4\pi}{3}\rho_0(\varepsilon_\text{pp}+\varepsilon_\text{CNO})(0.2R)^3 \end{align}\)
Vi har at
\(\begin{align} \varepsilon_\text{pp}&=2.3\cdot10^{-5}\,\text{W kg}^{-1}\\ \varepsilon_\text{CNO}&=2.6\cdot10^{-7}\,\text{W kg}^{-1} \end{align}\)
Dette gir oss en luminositet på \(7.2\cdot10^{23}\,\text{W}\). I forrige innlegg fant vi at luminositeten er \(3.251\cdot10^{23}\,\text{W}\). Dette er en relativ feil på nesten 100 prosent. Grunnen til at vi får så stort avvik er selvsagt antagelsene våre. Uniform tetthet er langt fra sannheten når det kommer til den virkelige verden. Energien som transporteres ut av kjernen vil ikke "gli" pent og pyntelig gjennom alle lagene til stjerna. Det er det vi antar når vi antar uniform tetthet. La oss ta en titt på hva temperaturen blir, med den nye luminositeten. Vi har at
\(\begin{align} L&=4\pi R^2\sigma T^4\\ T&=\sqrt[4]{\frac{L}{4\pi R^2\sigma}} \end{align}\)
hvor \(\sigma\) er Stefan-Boltzmanns konstant (\(5.67\cdot10^{-8}\,\text{W m}^2\text{K}^{-4}\)). Vi finner at temperaturen nå er \(973.3\,\text{K}\), i motsetning til det vi vet at den skal være; \(7985\,\text{K}\). Her får vi en relativ feil på nesten 88 prosent. Igjen, handler dette om antagelsen om uniform tetthet, i tillegg til antagelsen om at temperaturen er konstant på hele overflaten. Det er den absolutt ikke.
I neste og siste innlegg skal vi ta for oss noe makabert. Nemlig døden. Mannen med ljåen har fått seg romskip.
Forrige innlegg << Neste innlegg >>