Kort oppsummert så er et bilde egentlig bare en samling av dotter jevnt fordelt utover en flate, der hver dott har blitt gitt en spesifikk farge. Alle disse enkelt dottene på overflaten vil så danne et bilde når det blir mange nok av dem. Hver av dottene er det vi kaller for en piksel, og er det man bruker for å definere størrelsen på et bilde. Så når man sier at man har et bilde på 64x64 piksler så betyr det at bildet inneholder 64x64 dotter med hver sin farge. Rent teknisk så er dottene kvadratiske og vil fylle ut et kvadrat med bare den designerte fargen for den pikselen.

Det neste som burde komme opp som et spørsmål burde være hva det er som bestemmer hvilken farge hver piksel skal ha, og hvordan disse blir justert for å skape alle fargene man trenger til et hvilket som helst bilde. Bilder bruker i stor grad tilnærmet system som det digitale skjermer bruker, eneste forskjellen er at farger oppfører seg forskjellig fra lys til farger på en overflate som maling. Ta for eksempel en TV, hvis du går nærme nok skjermen, "NB! ikke anbefalt å gjøre det", så vil du kunne se at bilde på skjermen egentlig bare er en samling av små lys av fargen rødt, grønt og blått. Disse sitter så tett på hverandre i et repeterende mønster og vil til sammen danne bilde som du ser på skjermen, ved å justere styrken på hvert eneste av disse små røde, grønne og blå lysene. Det samme skjer i et bilde bare med fargekoder, for hver eneste piksel i et digitalt bilde vil inneholde tre verdier, (R, G, B) som står for red, green, blue. Disse verdiene går fra 0 til 255, og kombinasjonen av verdiene fra de tre ulike fargene vil bestemme hvilken farge den gitte pikselen har. Ta for eksempel at alle har verdien 0, det betyr at pikselen blir svart, og hvis alle har 255, så blir det hvitt.
Vi vil her kun forholde oss til et filformat som heter png, og fargekodene vil være (R, G, B), det finnes nemlig andre måter å oppgi farger som data som vi ikke vil gå nærmere inn på, vi er fysikere vår kunst er ikke innenfor fargeteori. Kan du tenke deg hvorfor dette var viktig å få frem?
For å oppsummere kort.
Et bilde kan bli sett på som en annen måte å lagre data på, det er bare strukturert på en annen måte enn det vi er vant til å se. Hver piksel inneholder tre verdier (R, G, B) som betyr at man i praksis kan tenke på dottene i bildet ovenfor som en slags tabell med verdier i hver av dottene.
Fra simuleringen av partikkelboksen så nevnte vi array, en slags tabellform, som er det verdiene her vil være lagret i. Ved å lage et program som kan lese av denne array'en kan vi nå hente ut denne dataen som betyr at bilder kan bli tatt i bruk som et verktøy. Da er det bare å sette i gang med å eksperimentere med png formatet, det er bare en liten ting til som vi må innom før vi kan gå løs på bildene, nemlig noe som heter stereografisk projeksjon.
En av våre antagelser er at bildene vi tar er fra himmelen rundt oss, det vil si en kule med oss et sted i sentrum. Denne kulen med horisonten, bakgrunnen, vil vi kalle for himmelkulen. Det er nemlig et ganske problematisk geometrisk problem vi nå står ovenfor, som kartografer har vridd hodene sine rundt siden man ble enige om at jorden var rund. Hvordan representerer man noe som ligger på overflaten til en kule i et 2 dimensjonalt plan samtidig som man beholder den opprinnelige formen og størrelsen?
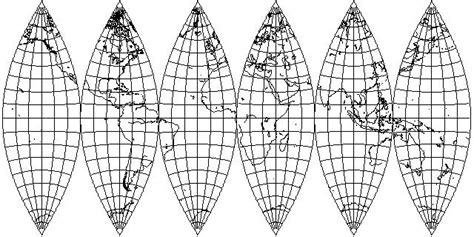
Essensen i problemet kan i stor grad bli oppsummert via et lite eksempel. Se for deg at du har en appelsin, la oss si at du har en tegning eller figur på dette skallet. En dag blir du lei av å måtte snu på hele appelsinen hver gang du skal beundre mesterverket ditt, så du bestemmer deg for å ta av skallet og legge det flatt på et bord med lik form som et rektangel. Resultatet du får burde likne litt slik som det er vist i neste bilde.
Man kan også tenke på det som å skulle få en badeball til å ligge helt flatt når den ikke har noe luft i seg. Det man ender opp med er at den alltid vil ha noe krumming.
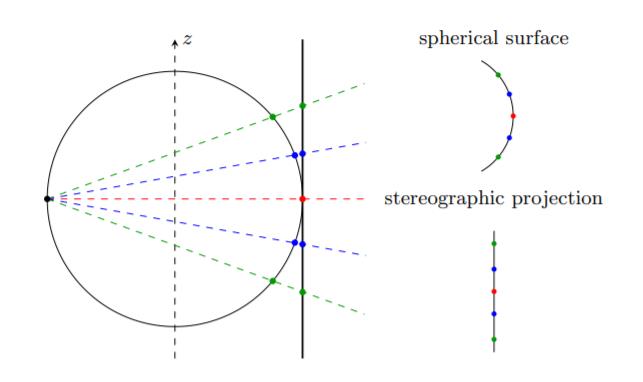
I vår projeksjon vil vi overføre bildet fra himmelkulen over til en flat overflate ved å ha et punk, der vårt kamera vil være, som vil ta et utsnitt av kulen, der størrelsen av utsnittet blir bestemt av kameraets FOV, field of view. Se for deg at vi sender et gitt antall stråler innenfor vårt FOV, disse vil så treffe overflaten på kulen, og vi vil hente ut verdiene som den pikselen en gitt stråle treffer, og plassere en ny piksel med samme verdi som den pikselen på kulen hadde for den gitte strålen, på en flat overflate bak. Denne overflaten vil stå normalt for overflaten fra en stråle som går fra sentrum av vår FOV til himmelkulen.
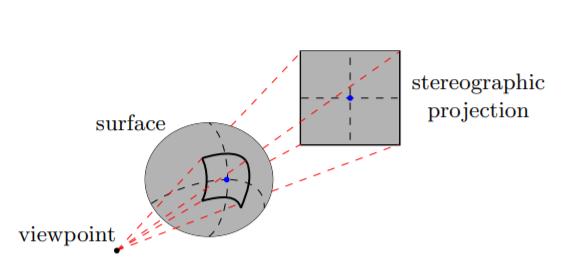
Dersom du er interessert i å vite mer så kan vi anbefale å se 3Blue1Brown sin video om But why is a sphere's surface area four times its shadow? Det som er mest relevant for dette er rundt 3 minutter merket.
Vi vil nå gjøre noe som kalles for koordinattransformasjon som vil si at vi bytter om på type koordinatsystem som blir brukt. I vårt tilfelle så går vi fra et sfærisk koordinatsystem til et kartesisk koordinatsystem, der kartesisk er det vanlige koordinatsystemet man er vant til å bruke.
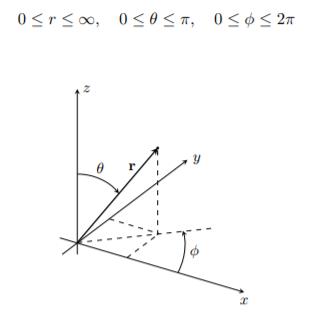
Fra tidligere innlegg vet vi at min/maks verdier for x og y er gitt som
\(X_{max/min} = \pm \frac{2\sin{\left(\frac{\alpha_{\phi}}{2}\right)}}{1+ \cos{ \left(\frac{\alpha_{\phi}}{2}\right)}}\\ Y_{max/min} = \pm \frac{2\sin{\left(\frac{\alpha_{\theta}}{2}\right)}}{1+ \cos{ \left(\frac{\alpha_{\theta}}{2}\right)}}\) der \(-\frac{\alpha_{\phi}}{2} \leq \phi - \phi_0 \leq \frac{\alpha_{\phi}}{2} \\ -\frac{\alpha_{\theta}}{2} \leq \theta - \theta_0 \leq \frac{\alpha_{\theta}}{2}\)
og \(\alpha_{\phi} = \phi_{max}-\phi_{min} \\ \alpha_{\theta} = \theta_{max}-\theta_{min}\)
Heldigvis for oss så trenger vi ikke å tenke så mye over de to siste delene, for vi vet, får oppgitt, at \(\alpha_{\theta} = \alpha_{\phi} = 70^o \) som gir oss at \(X_{max/min} = Y_{max/min} = \pm 0.63\), vi vet også at \(\theta_0 = 90^o \) og at \(\phi_0 = 0^o\). X og Y max/min sier oss hvilke verdier på overflaten vi prosjekterer over vil ha.
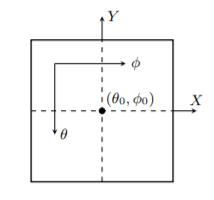
Videre har vi også den følgende forholdet som kommer fra transformasjonen
\(\theta = \theta_0 - \arcsin{\left[\cos{\beta}\cos{\theta_0}+\frac{Y}{p}\sin{\beta}\sin{\theta_0}\right]}\\ \phi = \phi_0 + \arctan{\left[\frac{X\sin{\beta}}{p\sin{\theta_0}\cos{\beta}-Y\cos{\theta_0}\sin{\beta}}\right]}\\ p = \sqrt{X^2+Y^2}\\ \beta = 2\arctan(\frac{p}{2}) \)
som gir oss den korresponderende vinkelen som et punkt på himmelkulen har gitt X og Y. Det vil si at vi kan ta et punkt innenfor våre \(X_{max/min} \) og \(Y_{max/min}\) verdier og få ut hvor på himmelkulen dette ville ha vært.
kort oppsummert
Vi vil lage et bilde ved å gjøre en koordinattransformasjon fra sfærisk koordinatsystem som er himmelkulen, og overføre pikslene derifra ned på et kartesisk koordinatsystem i xy planet. Ved å bruke oppgitte forhold kan vi få ut posisjonen til en piksel gjennom å vite hvor på himmelkulen vi ser på, og posisjonen i vårt xy plan gjennom x og y verdiene. Alt vi trenger å gjøre blir da å overføre verdien til den gitte pikselen fra himmelkulen over til de x og y verdiene vi brukte. Ved å gjøre dette på en systematisk måte vil vi til slutt få et bilde som da er resultatet etter en stereografisk projeksjon.

Da har vi det vi trenger for å utføre vår projeksjon, vi starter med å hente ut vårt referansebilde for å vite hvilke dimensjon, størrelse, det er i. Dette gjøres ved å importere bildet inn til python for så å lese av formen på array'en som alle piksel verdiene er lagret i, fra dette finner man ut at bildet har en størrelse på 640x480 piksler. En annen metode man kunne ha brukt er via paint og telle pikslene manuelt, men det er tungvint.
Deretter finner vi \(X_{max/min} = Y_{max/min} = \pm 0.63 \) som vi gjorde ovenfor, og det vi bruker dette til er å lage et slags rutenett som en slags oppdeling. Oppdelingen blir da 640 ruter for bredden og 480 ruter for høyden, for dette er da plasseringene for hver piksel vi skal bruke. Vi vet koordinatene allerede, for dette er plasseringen til hver av boksene i xy planet, og med det så legger vi inn formlene ovenfor og setter inn hver x og y verdi fra rutenettet. Det vi får er at x og y verdiene byttes ut med \(\theta \) og \(\phi\) som korresponderer til den gitte x og y verdien. Dette bruker vi igjen ved å hente ut verdien som en gitt piksel har for en gitt \(\theta \) og \(\phi\) fra himmelkulen. Sluttresultatet er at vårt tomme rutenett nå inneholder (R, G, B) verdien fra himmelkulen i sine korresponderende posisjoner.
Vi ble også nødt til å flippe det fra høyre til venstre for så å rotere det \(180^o\) på grunn av at det ikke var riktig rotert fra uthenting av verdiene. Et bilde er så og si det samme bilde så lenge man ikke endrer på hva verdiene er i forhold til pikslene rundt, så man kan rotere, og speile det om uten at det har noe å si.

Panorama?
For videre referanser vil det være nyttig å ha et bilde for hver hele vinkel \(\phi\) som dekker \(360^o\). Det vil si at vi gjør en hel rotasjon og tar et bilde for hver hele vinkel, dette kunne vi ha gjort manuelt, men det er tungvint, så vi lagde heller en liten modul som gjorde det for oss. Lagde også en egen kode-del som lagde filnavnene for oss slik at vi slapp å skrive panorama0000.png helt til panorama0359.png manuelt. Tallet som kommer etter panorama indikerer hva vinkelen \(\phi\) er for det gitte bilde, så panorama0000.png vil ha en vinkel \(\phi = 0^o\).
Litt mer avansert konsept for smak og behag
Selv om vi lager bildene automatisk uten at vi trenger å skrive filnavnene manuelt så tar det fremdeles, relativt, lang tid å lage alle bildene. Vi valgte derfor å tilpasse koden slik at den kunne gjøre noe som kalles for parallellisering av prosessen. Parallellisering er når vi får en kode til å gjøre flere ting på en gang, og det er ulike former for parallellisering, men vi brukte en av de enklere metodene, som er multiprosessing.
En pc har noe vi kaller for prosessor kjerner og antallet varierer fra pc til pc. Under vanlige omstendigheter vil en kode bare bruke en av disse kjernene nå den kjøres, mens de andre ikke blir brukt. Multiprosessing er egentlig at vi bruker av flere av disse kjernene når koden kjøres, dette vil da dele på arbeidsmengden som hver kjerne må gjøre, og dermed redusere tiden.
For å visualisere dette kan du tenke deg at du jobber i en butikk og at du sitter bak kasseapparatet. Det er bare du som tar i mot kunder akkurat nå, så køen med kunder vil da bli lang, fordi vi antar at butikken har mange kunder. La oss si at det tar deg 10 minutter på å gjøre deg ferdig med alle kundene, som blir da tiden det tar å kjøre en kode. Neste dag så har du en medarbeider, som er like effektiv som deg, og med like mange kunder som dagen før vil køen bli fordelt på to. Tiden det nå tar å bli ferdig med alle kundene blir totalt 5 minutter.
I eksempelet blir da en kjerne deg som tar imot kunder, og kundene representerer arbeidsmengden som må gjøres. Multiprosessing er dermed en metode som kan gjøre koden raskere ved å dele opp arbeidsmengden på flere kjerner. Det er selvfølgelig mer detaljer bak det hele som at det som gjøres må være uavhengig av hverandre, og at alt må samles før man kan fortsette videre i koden, men det er ting som vi ikke trenger å gå i detalj for nå.
Tanken bak å skulle gå gjennom bryet med å gjøre det mulig å bruke flere kjerner samtidig for å lage alle de 360 bildene var at det skulle gå raskere å lage dem dersom vi måtte endre på noe, som for eksempel størrelsen eller endre på noen av vinklene. Under er det en video som viser resultatet etter at bildene har blitt satt sammen.
Forrige innlegg finner du her
Neste finner du her