Vi er interessert i den radielle hastigheten til vår rakett i forhold til stjernen vår, og for å finne det har vi om bor på raketten utstyr som gir oss informasjon om den mottatte bølgelengden fra to stasjonære stjerner på stjernen våres og som vi mottar på raketten. Ved å bruke Doppler effekten kan man finne ut av hvordan stjernen vår beveger seg i forhold til referansestjernene, og hvordan raketten beveger seg i forhold til referanse stjernene.
Før vi går løs på å bruke den gitte informasjonen til å finne den radielle hastighetskomponentene til raketten kan det være lurt å gå igjennom konseptet bak å bruke Doppler effekten. Jeg vil spare deg for bruken av passerende ambulanse, bil eller tog til å beskrive Doppler effekten.
I gif'en under kan vi se tre blå sirkler, kilder, som sender ut bølger. Vi kan her se for oss at bølgene er EM-stråling som blir sendt ut fra referanse stjernene. Doppler effekten er sammenpressingen eller forlengelsen av bølgene avhengig av bevegelsen til kilden i forhold til retningen bølgene blir sendt ut i.
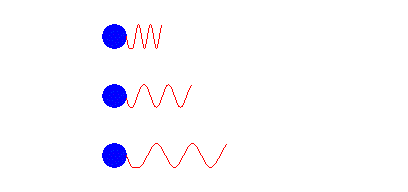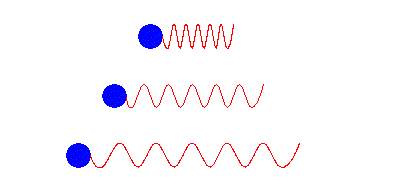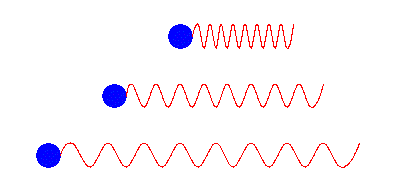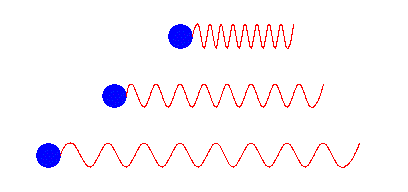

Vi vil si at \(\lambda_0\) er bølgelengden som vi måler dersom dersom det ikke er noe bevegelse mellom observatøren og kilden. I vårt tilfelle er \(\lambda_0 = 656.3 \ nm\), som er bølgelengden til \(H_{\alpha}\), det vi måler fra referanse stjernene. \(H_{\alpha}\) er den bølgelengden som fotonet har når et elektron fra helium går fra sitt 3. energinivå, ned på det andre energinivået.
For å finne farten vi en gitt observatør har i forhold til en referanse stjerne kan bli funnet ved å bruke
\(\frac{\lambda - \lambda_0}{\lambda_0} = \frac{v_r}{c}\Rightarrow \frac{c \cdot (\lambda - \lambda_0)}{\lambda_0} = v_r\) der \(c\) er lysets hastighet i vakuum. Vi kan si at \(\Delta \lambda = \lambda - \lambda_0\), så når \(\Delta \lambda\) har negativ fortegn så betyr det at observatøren og kilden beveger seg mot hverandre, og positivt fortegn så beveger de seg fra hverandre. Vi måler dermed mottatt forskyvning i bølgelengde opp mot en referanse som er \(H_{\alpha}\).
Ved å bruke vårt utstyr for å få \(\Delta \lambda\) fra hver av referanse stjernene i forhold til vår egen stjerne og rakett så vet vi kun hvordan stjernen og raketten beveger seg i forhold til referanse stjernene. Vi ønsker å finne ut av hvordan raketten beveger seg i forhold til vår egen stjerne. For å finne ut av dette kan vi bryte ned konseptet vi vil bruke fra 2 dimensjoner ned til en dimensjon.
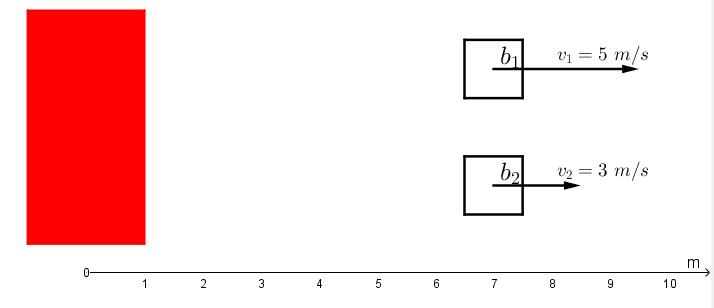
Vi og en annen medstudent, eller venn, har hver våres biler, og en dag bestemmer vi oss for å kjøre over en rett strekning for å teste diverse utstyr. Grunnen til at vi kjører er ikke så viktig, det som er viktig er måten vi måler farten til de to bilene. Utstyret som er montert i bilene gir oss farten i forhold til vårt referanse objekt som i dette tilfelle er en bygning.
Når vi setter i gang kjører begge fra objektet i samme retning som vi har definert som positiv retning, og fra apparatene i bilene vet vi at vi kjører med en hastighet på \(v_1 = 5 \ m/s\), og vår venn ved siden av kjører med en hastighet på \(v_2 = 3\ m/s\). Nå bytter vi referansesystem for vi er interessert i å vite hvor fort vi kjører i forhold til vennen våres, så det betyr at hele systemet nå beveger seg med \(b_2\), bilen vår venn kjører. For å finne hvor fort vi nå kjører i det nye referansesystemet så må vi vite hvor fort referansesystemet, \(b_2\), beveger seg for så å ta vår egen hastighet og trekke fra hastigheten som systemet beveger seg med. Dette gir oss at vår hastighet, \(V\), i forhold til \(b_2\) er \(V = v_1 - v_2 \Rightarrow 5 -3 \Rightarrow V = 2\ m/s\). Se gjerne på illustrasjonen over for det viser det som nettopp ble forklart. Dette er måten vi vil finne hastighetskomponentene til raketten i forhold til stjernen vår.
Vi vil ha 2 hastighetskomponenter, en for hver av referansestjernene. Vi vil si at origo er plassert i sentrum av vår egen stjerne, og vi vet også, ut fra observasjoner, vinkelen som de to referansestjernene har med x-aksen. Vi er nå nødt til å gjøre nok en koordinat transformasjon, der vi nå har en linje gjennom origo, stjernen vår, som går gjennom hver av de to referansestjernene. Dette blir våre nye akser som så må bli rotert om aksene slik at hver av stjernene har samme vinkel i forhold til x-aksen som de hadde i det vanlige koordinatsystemet. Vinklene stjernen har i forhold til aksene er for den første stjernen \(\phi_1 = 97.2^o\) og for den andre stjernen \(\phi_2 = 348.5^o\). Rotasjonen blir da som følger vist i videoen under.
Vi ser for oss at begge stjernene starter på samme sted og på grunn av konvensjon så vil vi rotere \(\phi_2\) mot klokken og \(\phi_1\) med klokken. De oransje punktene representerer referanse stjernene, og pilen på de fargede linjene indikerer hva som blir definert som positiv retning. Den blå punktet i origo er vår stjerne. Verdt å merke seg er at dette ikke er riktig skalert, for det er ment til å illustrere hva som skjer. Vi kan også anse \(\phi_1\)som vår x-akse og \(\phi_2\) som y-aksen i det transformerte koordinatsystemet.
Grunnen til at man går gjennom bryet med å transformere koordinatsystemet er at man da slipper å måtte dekomponere hastigheten man får ut etter å ha funnet ut hastigheten vi, eller stjernen, beveger seg i forhold til referanse stjernene. Sånn sett gjør det utregningen letter ved å slippe å måtte ta hensyn til retningen den målte \(\Delta \lambda\)har utenom når man transformerer det tilbake til det vanlige koordinatsystemet.
For å transformere, rotere, fra det vanlige koordinatsystemet til det andre så har vi følgende rotasjons matrise
\(\begin{pmatrix} d_1 \\ d_2 \end{pmatrix} = \begin{pmatrix}\cos{\phi_1} & \sin{\phi_1} \\ \cos{\phi_2} & \sin{\phi_2}\end{pmatrix} \begin{pmatrix} d_x \\ d_y \end{pmatrix}\) her er \(d_x\) og \(d_y\) x og y verdien til et punkt i det vanlige koordinatsystemet, når man putter det inn i resten av uttrykket sammen med vinklene for referanse stjernene så vil matrisen rotere på koordinatsystemet og dermed også flytte punktet til sin tilsvarende plass i det nye systemet. Dette kan gjøres baklengs også, at vi har \(d_1\) og \(d_2\) verdiene, som vi så setter inn og får ut de vanlige verdiene for det normale koordinatsystemet. Dette får vi gjennom å bruke følgende formel
\(\begin{pmatrix} d_x \\ d_y \end{pmatrix} = \dfrac{1}{\sin{(\phi_2 - \phi_1)}}\begin{pmatrix}\sin{\phi_2} & - \sin{\phi_1} \\ - \cos{\phi_2} & \cos{\phi_1}\end{pmatrix} \begin{pmatrix} d_1 \\ d_2 \end{pmatrix}\)
vil du lære mer så har 3Blue1Brown en video for dette temaet som du kan finne her.
Noe som er verdt å merke seg er at på grunn av at avstandene mellom raketten til referanse stjernene, og vår egen stjerne til dem ser så utrolig store i forhold til avstanden fra raketten til vår egen stjerne, så trenger vi ikke å ta hensyn til noen vinkler for å dekomponere hastigheten man får fra hver enkelt måling. Det betyr at når vi finner vår radielle hastighet i forhold til vår egen stjerne så kan vi trekke hastigheten stjernen har i forhold til referanse stjernene fra vår raketten sin hastighet før vi transformerer om komponentene tilbake til det vi ønsker.
Det vi nå gjør for å finne hastigheten i forhold til vår egen stjerne så måler vi først \(\Delta \lambda\)fra hver av stjernene som vår egen stjerne og raketten mottar, deretter gjør vi det om til en hastighet komponent via å bruke \(\frac{c \cdot \Delta \lambda}{\lambda_0} = v_r\). Deretter tar vi komponentene til raketten og trekker fra med komponentene som vår stjerne har for så å bruke formelen for transformasjonen fra det roterte systemet tilbake til det vanlige for å få hastighet komponentene som raketten har i forhold til vår egen stjerne.
Utregningen blir som følger, starter med å finne komponentene for vår egen stjerne i det transformerte systemet
\(\left\{\begin{matrix} \Delta_s \lambda_0 = -0.00523 \\ \Delta_s \lambda_1 = \ \ 0.00793 \end{matrix} \right \} = \left\{\begin{matrix} v_{S_0} = -0.50 \\ v_{S_1} = \ \ 0.76 \end{matrix}\right\} \)
deretter for raketten
\(\left\{\begin{matrix} \Delta_r \lambda_0 = \ \ 0.0439 \\ \Delta_r \lambda_1 = -0.0547 \end{matrix} \right\} = \left\{\begin{matrix} v_{R_0} = -5.27 \\ v_{R_1} = \ \ 4.23 \end{matrix}\right\}\)
\(V = v_r - v_s \Rightarrow V = \begin{pmatrix} -4.76 \\ \ \ 3.47 \end{pmatrix}\) etter transformasjon får vi hastigheten for raketten \(V = \begin{pmatrix} -2.63 \\ \ \ 4.47 \end{pmatrix} AU/yr\)
NB! tallene som er gitt fra utregningen er det vi fikk ved å bruke den ekstra justeringen som blir snakket om i resten av dette innlegget.
En måte man kan sjekke om dette stemmer så kan vi se på et tilfelle der den mottatte \(\Delta \lambda\) som raketten måler er lik 0 så betyr det at raketten ikke beveger seg i forhold til stjernen. Det betyr derimot at raketten beveger seg like fort og i samme retning som vår egen stjerne beveger seg i forhold til referanse stjernene.
Dette kan vi også se om vi bruker vi utregningen ovenfor så vil \(V = 0\) som betyr at \(v_r = v_s\). Første gangen vi gjorde testen så fikk vi \(V = [-0, -0]\) og uten å gjøre justeringer så viste dette seg å gi oss hastigheten vi skulle ha, men med motsatte fortegn, så vi endret litt på rotasjons matrisen slik at vi skulle få riktig fortegn ved å gange inn \(-1\). Måten vi fant ut av dette var å tegne opp situasjonen og sammenlikne med det vi vet fra før av.
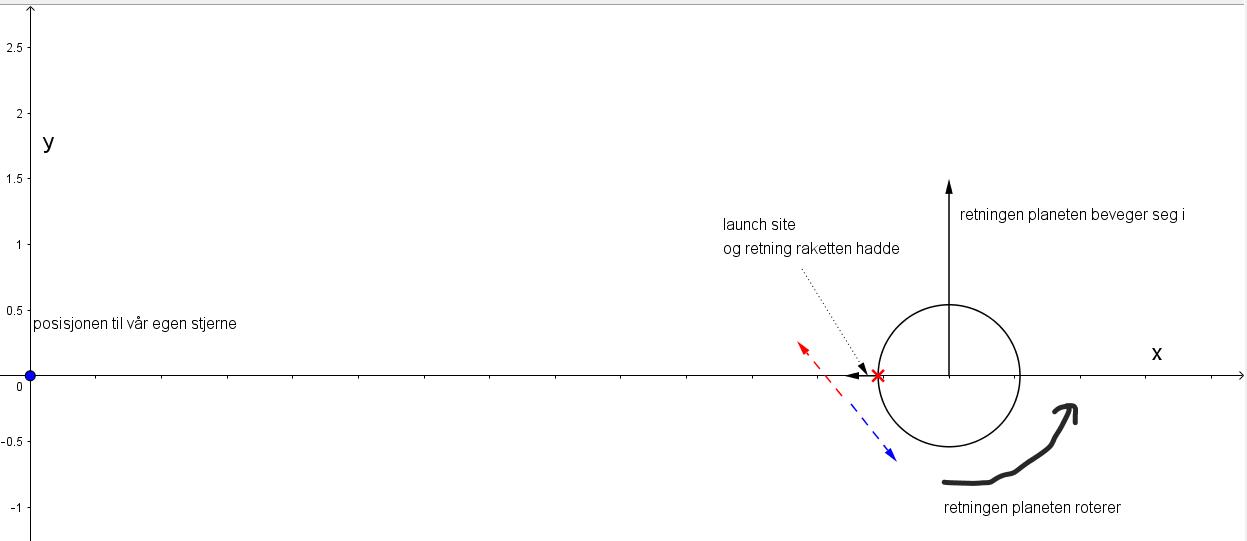
Vi vet fra før av at planeten roterer mot klokken og bruker mer enn 24 timer på å gjøre dette, det betyr at hastigheten raketten får fra rotasjonen alene ikke er så stor. Vi hadde oppskytningen rettet mot vår egen stjerne, og det tok rundt 572 sekunder. På grunn av tiden det tok å skyte opp, i forhold til tiden det tar for planeten å rotere rundt sin egen akse, så vil bidraget fra rotasjonen være veldig liten på grunn av hvor mye den rekker å rotere på den korte tiden. Vi vet også retningen planeten går i bane rundt stjernen, og det er her en del av hastigheten i y retning vil komme fra.
Dette er informasjon vi vet fra tidligere innlegg, og bildet under viser oss situasjonen. Hastighet vektoren, som er de rød og blå pilene, er våre målte radielle hastighet ved bruk av Doppler metoden fra dette innlegget. Den blå vektoren er fra det vi fikk første gangen uten å rette opp i fortegn. Vår største indikasjon på at dette må være feil er retningen for x komponenten. Den blå har denne pekende inn mot planeten som er i motsatt retning av det vi hadde for oppskytingen. Y komponenten er også i feil retning ettersom vi hovedsakelig skøyt rett opp fra overflaten, som betyr at vi ikke har noe som gir en hastighet i y retning utenom rotasjonen og bevegelsen til vår egen planet. Når fortegnet ble snudd ga det oss den rød vektoren, som er langt mer rimelig retning for hastigheten. Her er da retning for både x og y komponenten i riktig retning. Y komponenten kommer av at bevegelsen til planeten er langt større enn det rotasjonen ville ha bidratt med i y retning. X komponenten på grunn av retningen vi skøyt opp raketten i.
\(\begin{pmatrix} d_x \\ d_y \end{pmatrix} = - \dfrac{1}{\sin{(\phi_2 - \phi_1)}}\begin{pmatrix}\sin{\phi_2} & - \sin{\phi_1} \\ - \cos{\phi_2} & \cos{\phi_1}\end{pmatrix} \begin{pmatrix} d_1 \\ d_2 \end{pmatrix}\)
Med dette så fikk vi den hastigheten vi skulle ha.
Forrige innlegg finner du her
Neste innlegg finner du her