Nå som vi har kommet fram til planeten, kan man jo lure på hva som egentlig forteller oss at banen vår er stabil? Vi kunne jo godt ha bare prøvd oss fram, men vi har ikke all drivstoffet i verden! La oss dra frem noe kjent, tolegemeproblemet.
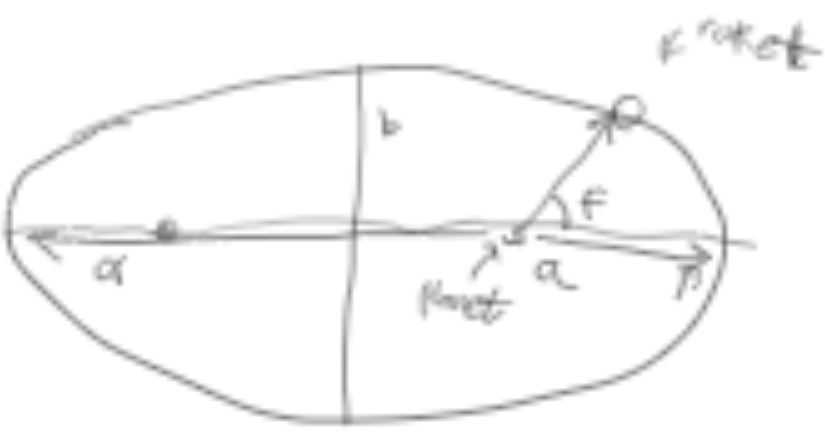
Vi ser så for at vi skal vite hva vår bane vil være, må vi vite hvor stor den lille og store halvaksen er. For å finne disse må vi dra frem en del likninger som kan virke litt fjernt:
\(e = \sqrt{1-(\frac{b}{a})^2} \\ p = \frac{b^2}{a} \\ p = \frac{h^2}{m} \\ p = a(1-e^2) \\ r = \frac{p}{1+e\cos{f}}\)
Disse er formlene vi kjenner for en ellipse, og kan så bruke de til å finne det vi mangler. Men hva var nå h igjen? Jo, fra når vi snakket om keplers lover er jo dette spinnet. Den eneste verdiene vi kjenner blir derfor r og h. Målet blir å få en så sirkulær bane som mulig, ettersom dette vil gi oss en stabil fart. Vi gjør en antakelse at energien er bevart i systemet, og vil så ha at eksentrisiteten (forholdet mellom lille og store halvakse) er 0. På dette vis vil vi ha en perfekt sirkel, hvor a = b.
Vi bruker dette problemet når vi ser på to objekter hvor det kun er en tyngdekraft som fungerer, vi ser bort ifra andre gravitasjonskrefter enn planeten vår fordi at tyngdekraften til planeten vår er langt større. Dette gir oss så at energien i problemet er:
\(E = \frac{1}{2}\hat{\mu}v^2 - G\frac{\mu (m_p+m_r)}{r^2}\)
Hvor farten er lengden av den radielle og tangentielle farten, her vil vi helst ha en så liten radiell hastighet som mulig da dette vil få oss nærmere planeten. Vi finner farten ved:
\(v = \sqrt{v_x^2+v_y^2} = \sqrt{v_r^2+v_\theta^2}\)
Når vi løser for denne energien en gang, kan vi bruke den videre da vi antok at energien var konservert. Vi setter så inn formelen for r, og gjennom en del algebra ved at energien er konservert, kan skrive energien på følgende måte.
\(r = \frac{p}{1+e\cos{f}} \\ E = -G\frac{\mu (m_p+m_r)}{2p}(e^2-1)\)
Men vent! Negativ energi? Jo, hvis du husker, så er energien negativ om den potensielle energien dominerer. I tolegemeproblemet, vet vi at for at en bane skal være stabil, må dette være sant. Hvis den kinetiske hadde dominert, ville jo raketten bare flydd videre langt vekk fra planeten! Dette er en grunn til at vi bør bremse ned farten rett før planeten, slik at tyngdekraften kan ta hånd om oss. Vi setter så inn likningen for p for å finne den store halvaksen.
\(p = a(1-e^2) \\ E = -G\frac{\mu (m_p+m_r)}{2a(1-e^2)}(e^2-1) \\ a = -G\frac{\mu (m_p+m_r)}{2E}\)
Det er så nesten hele problemet løst! I allefall det vanskeligste, fra her er det jo bare å bruke likningene fra en ellipse til å finne de andre ukjente verdiene. Vi mikser og trikser med det vi vet:
\(p = \frac{b^2}{a} \\ p = \frac{h^2}{G(m_p+m_r)} \\ b = h\sqrt{\frac{a}{G(m_p+m_r)}}\)
Ved den store og lillehalvaksen kan vi så finne eksentrisiteten til banen:
\(e = \sqrt{1-(\frac{b}{a})^2}\)
Vi kan også finne omløpstiden vår ved Keplers tredje lov:
\(P = \sqrt{\frac{4\pi^2}{G(m_p+m_r)}a^3}\)
Da skulle det være alt vi skulle trenge for å vite noe om banen vår! Målet vårt blir jo å få en så perfekt sirkulær bane som mulig, og må da ha eksentrisiteten til å være null.
Det er jo klart at disse likningene vil gi litt avvik fra å anta energien er konservert, det er ikke helt et tolegemeproblem ettersom det er mange flere planeter som kan ha innvirkning på banen vår. Likevel så har vi nå vist at vi kan finne banen vår så lenge vi kjenner energien vår.