It's so crazy to think that we're sooo close to launching our spacecraft now! Finally we are fleeing from Chichiyaku!!

In previous post we designed our software to determine angular orientation, analyse spacecraft velocity and analyse spacecraft position. The only remaining part is to create a simulation of our spacecraft during its voyage in space. We do this to visualise how the rocket will float in space.This will help us during planning the voyage, to visualise when a boost is needed and how much in order to correct the spacecraft's path. You know... to avoid floating uncontrolled in space :)
I mean you wouldn't go backpacking around the world without planning, right? This is exactly like that.
How is this simulation done you may ask? Let's consider our spacecraft floating in space. Its movement will be affected by bodies in space. That is in fact because of PLANETS! Surrounding planets have a gravitational force pulling on our spacecraft.
A quick refresh. Newton's gravitational law is given as
\(\vec{F} =-\gamma \frac{mM}{|\vec{r}|^3}\vec{r}\), constants and variables are described in this document from post "THINGS YOU WISH YOU KNEW B4 YOU LAUNCHED."
By calculating the gravitational force from every planet in our solar system, we can find an expression for our spacecraft's acceleration using Newton's second law of motion \(\vec{F} = m\vec{a}\).
And the expression for spacecraft's acceleration is..
-
-
-
-
-
-
-
\(\vec{a} = -\gamma\frac{mM_s}{|\vec{r}|^3}\vec{r}- \sum_{i=1}^N \gamma\frac{mM_i}{|\vec{r}-\vec{r_i}|^3}(\vec{r}-\vec{r_i})\)
Oh yes, quite a mouthful. Essentially, the acceleration of the spacecraft at a given position is affected by the gravitational force from the sun, in addition to the gravitational force from the other planets. Note how we mentioned "at a given position". This is because the gravitational force is dependent on \(\vec{r}\)(being the distance between the rocket and bodies in space). But the distances vary depending on where the spacecraft is in space!!
(Check here for a more detailed math section of spacecraft's acceleration AND BEAUTIFUL DRAWINGS)
Now we are ready to simulate the spacecraft acceleration, velocity and position using Euler Cromer!
Sounds familiar? We did discuss the Euler's method in post "DIY ROCKET SHIP!!". There is a slight difference between Euler's method and Euler Cromer, but they build on the same concept which can be read in the post linked above.
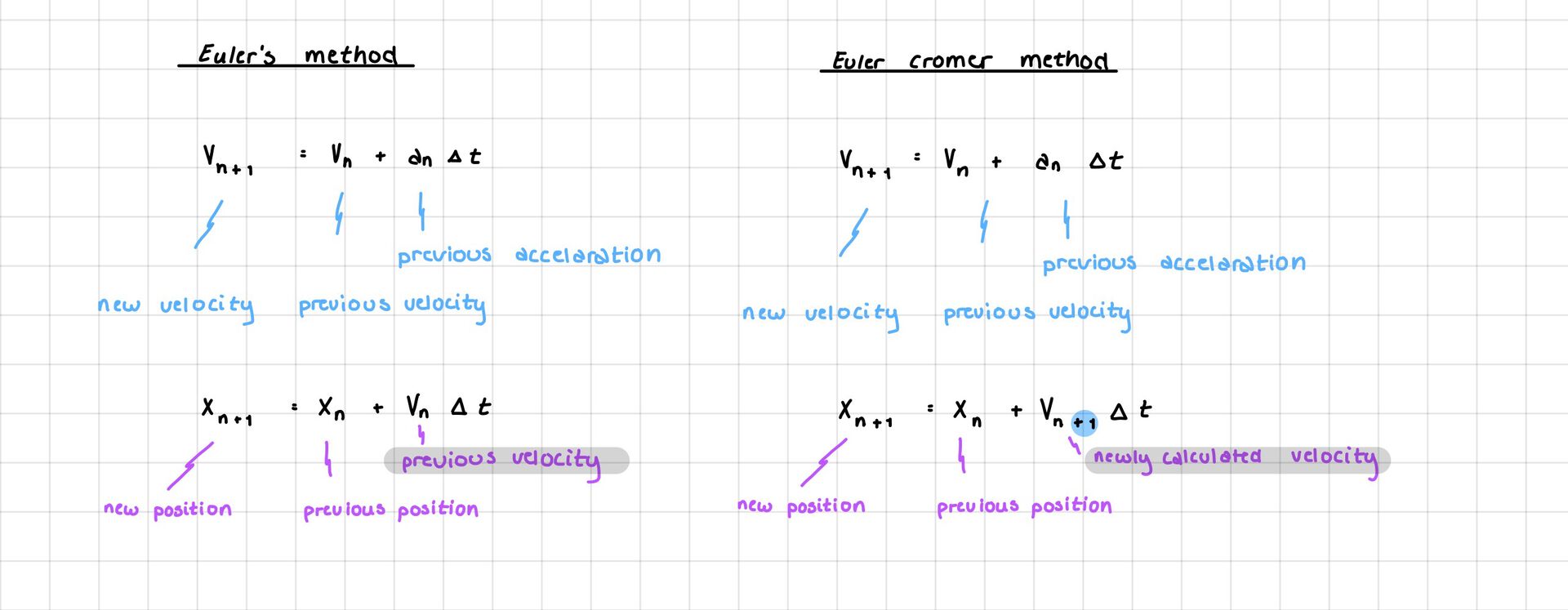
We solve this method by reading from top to bottom, meaning the way the equations are written is the order we solve them. Usually we simulate over a time period, \(\Delta{t}\) is the time step dividing the time period into smaller pieces. This means we calculate the position, velocity and acceleration for all of these small time steps along the time period. For example simulate for 10 min and calculate values every 30 seconds.
The difference in the two methods can be seen in how a new position is calculated. Instead of looking at previous velocity in order to calculate the new position like Euler's method, the newly calculated velocity is used instead in Euler Cromer. Hmmm okay so what does that mean?
Rebecca: This is getting boring. Can we get some pictures in here?
Karl: Sure we can! Oh Lightning McQueen, could you give us a hand?
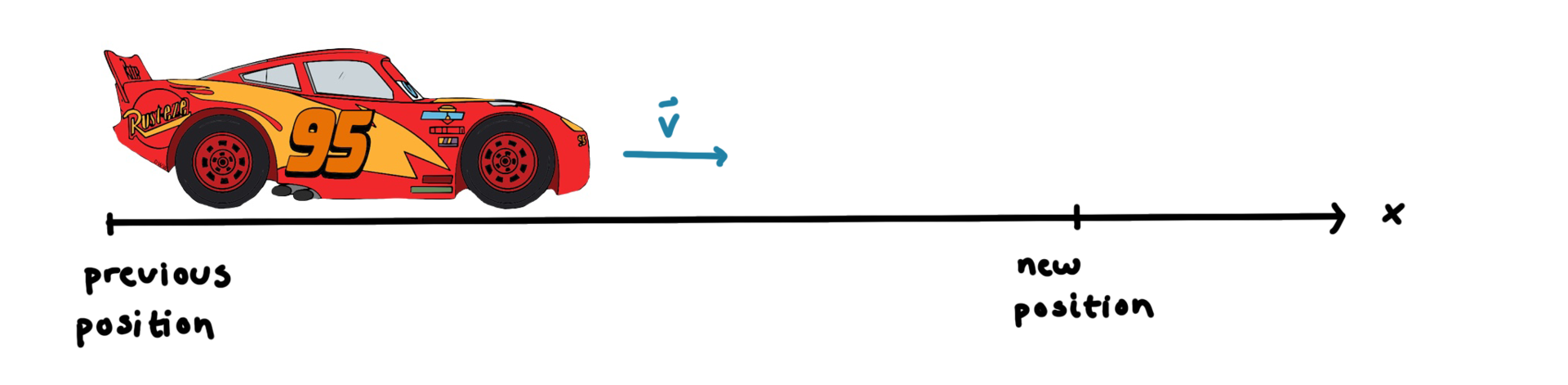
How would moving Lightning McQueen calculate his next position at next time step \(\Delta{t}\)?
Method 1: Check his speedometer for velocity at previous position. Calculate new position after time \(\Delta{t} \rightarrow\) \(x_{new} = x_{previous} + v_{previous} \cdot \Delta{t}\).
Then drive for a time \(\Delta{t}\) to \(x_{new}\).
Method 2: Start at previous position, drive for a time \(\Delta{t}\), check speedometer for his velocity at new position. Calculate where he ended up after driving for a time \(\Delta{t}\)\(x_{new} = x_{previous} + v_{new}\cdot\Delta{t}\)
Just by using speed triangle equation, both Euler's method (method 1) and Euler Cromer (method 2) falls right out. That wasn't so hard to understand. Thank you Lightning McQueen!!
Unfortunately, Euler cromer is not the most accurate numerical integration method. Other methods are way more accurate for example Runge Kutta 4th order (the simplicity here though, is non-existent. You can read more about the method here.) Unlike leap frog, Euler Cromer does not conserve energy in the system. The consequence is that you cannot calculate "backwards" and expect the same values.
BUT the method does its job well enough and it is a very simple method to implement in the computer, sooo...
Karl: To the computer!!

Rebecca: BUT GOD FUCKING DAMMIT. THE INTERN AGAIN!
Karl: Hmmm.. maybe we should stop accepting interns. They keep messing up our code.
Okey, so let's just pretend we have an idea of how the voyage may look instead. Now we need to think of boosts! What is that you may ask? It is a push given to the rocket to correct its path and guide it towards the destination planet. We do that by adding a change in velocity \(\Delta{v}\) at a certain time.

Think of it like this: You know those shopping carts in the grocery store? Yes, those who are very hard to push sometimes. You are calmly pushing the cart in between two aisles looking for cornflakes. You cart starts swerving slightly out of its path and headed towards a tower of stacked cans. SHIT NO GOOD! You use your body strength to push it away and ahh... it' now back to its path in between two aisles.
That push maneuver you just did, oh yes that was a boost :) A boost however, can change both direction and speed. Let's look at different types of boost.
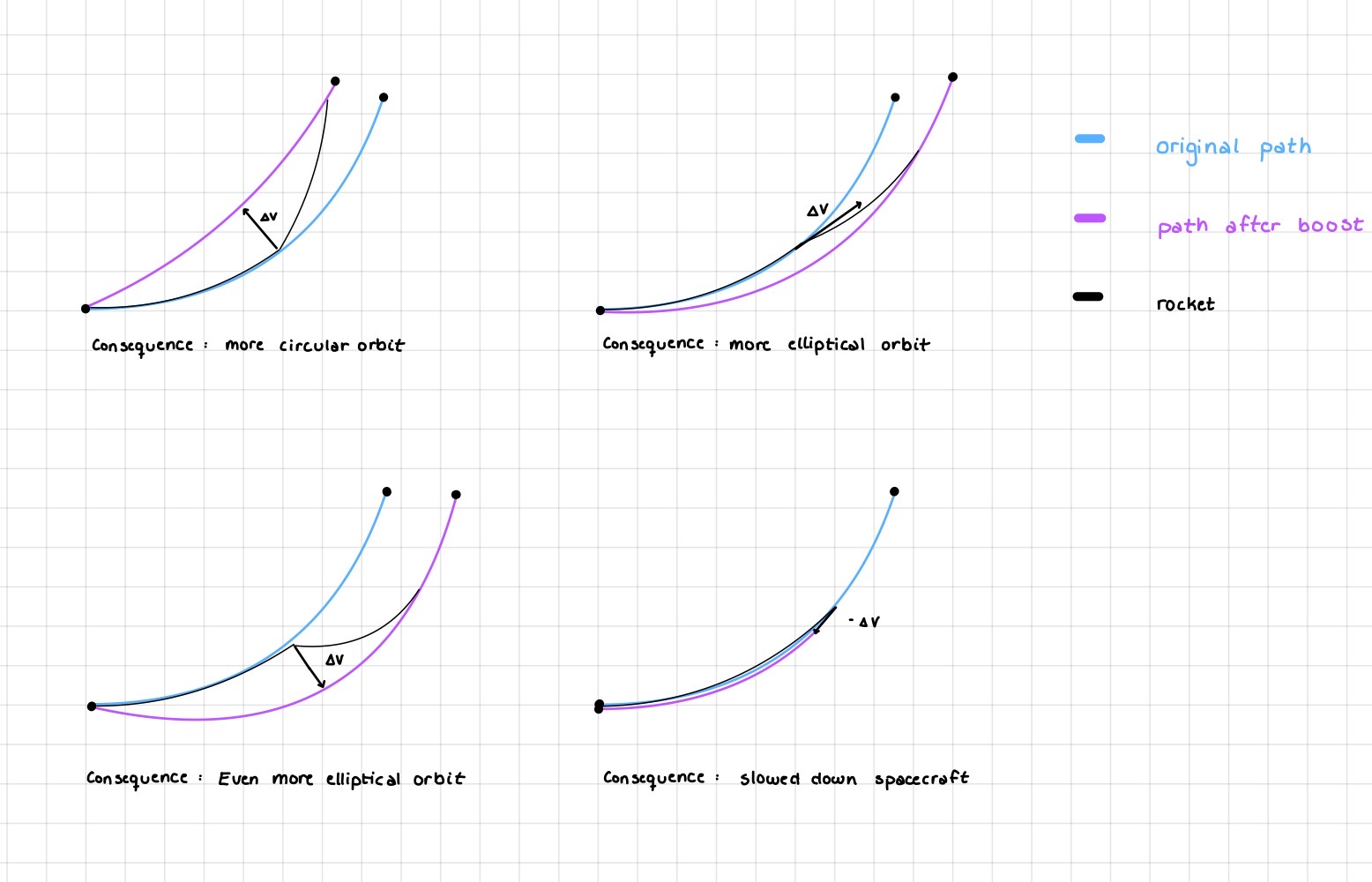
Upper left corner: (Left) Tangential boost on direction of velocity.
Bottom left corner: (Right) Tangential boost on direction of velocity.
Upper right corner: Boost with direction of velocity.
Bottom right corner: Boost against direction of velocity.
We boost by sending commands to our spacecraft. The response we get from the spacecraft will include how much fuel was used to boost. Looks something like this:
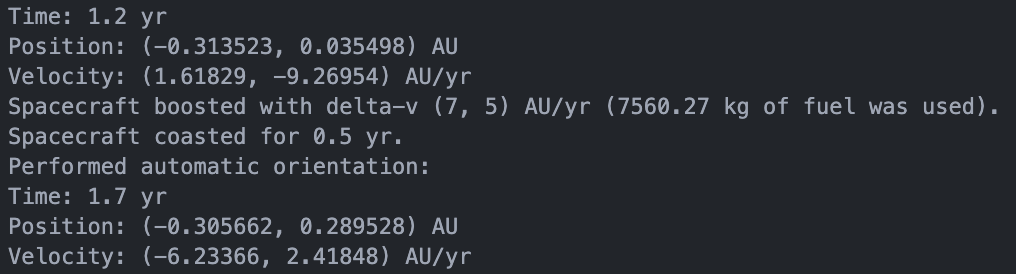
Easy peasy lemon squeezy. For our output we see the voyage began at year 1.2. After that we boost in both positive x and y direction and use 7560.27 kg fuel and coast for 0.5 year before we check for position and velocity after coasted period. This is just an example of how it looks for us on the computer and numbers shown are just test parameters.
Ps. we will assume a boost will happen instantaneous. After launch we have 11179.kg fuel. Depending on how much we decide to boost, we might have to increase the amount of fuel before launch.
Plan for actual launch and voyage may look something like this:
\(t = \text{start time}: \text{launch from $\vec{r}_0$ = $\vec{r}_{planet} $+ (x, y)}\)
\(t = \text{some time}: \text{boost $\Delta{\vec{v}}= (x, y) $ AU/yr}\)
I would have given you all a detailed plan if our intern didn't decide to sabotage stuff again...
Rebecca: Ugh, I'm tired. Karl could you take over from here?
