Introduksjon
Det svever rundt 30 satellitter over hodene deres på jorda hele tiden. Det er satellitten som er sendt opp av USAs forsvar, og som brukes til å navigere. Med høy nøyaktighet kan de beregne posisjonen til en mottaker i nesten all slags vær. I dette innlegget skal vi forsøke å gå grundig til verks for å vise hvordan satellittene er underlagt relativistiske effekter.
Situasjonen
Vi befinner oss på vår hjemplanet. Over hodene våre svever to satellitter. De sender hele tiden et signal til vår mottaker, med tiden de sendte det ut og posisjonen deres. Når vi starter eksperimentet er alle klokkene synkronisert. Etter hvert som tiden går vil vi undersøke om posisjonen vi får oppgitt fra satellittene stemmer overens med det vi vet at den skal være. Her har vi gjort noen antagelser:
- Planeten roterer ikke om sin egen akse. Altså vil vår posisjon forbli uendret hele tiden.
- Satellittene beveger seg i en sirkulær bane.
Metoder
Newtons 2. lov
For å finne farten satellittene har, bruker vi Newtons 2. lov for sentripetalakselerasjon.
\(\begin{align} \Sigma F=m\frac{v^2}{r} \end{align}\)
hvor \(m\) er massen til objektet, \(v\) er farten langs sirkelbanen og \(r\) er avstanden til denne sirkelens sentrum. Siden vi vet posisjonen til satellittene, kan vi finne avstanden deres fra planetens sentrum. Vi bruker de første målingene vi får fra satellittene.
\(\vec{r}_1=[-3831.207, -3148.374]\,\text{km}\\ \vec{r}_2=[-1743.749, -4642.152]\,\text{km}\\ r_1=|\vec{r}_1|=4958.871\,\text{km}\\ r_2=|\vec{r}_2|=4958.854\,\text{km}\)
Kraftsummen er tyngdekrafta, som gir oss uttrykket for banefarta.
\(\begin{align} v=\sqrt{\frac{GM}{r}} \end{align}\)
Her er \(G\) gravitasjonskonstanten (\(6.67\cdot10^{-11}\,\text{m}^3\text{kg}^{-1}\text{s}^{-2}\)), \(M\) er massen til planeten (\(1.649\cdot10^{23}\,\text{kg}\)) og \(r\) er avstanden fra planetens sentrum. Med dette finner vi banehastigheten til hver av satellittene.
\(v_1=v_2=1.49\,\text{km/s}\)
Cosinusloven
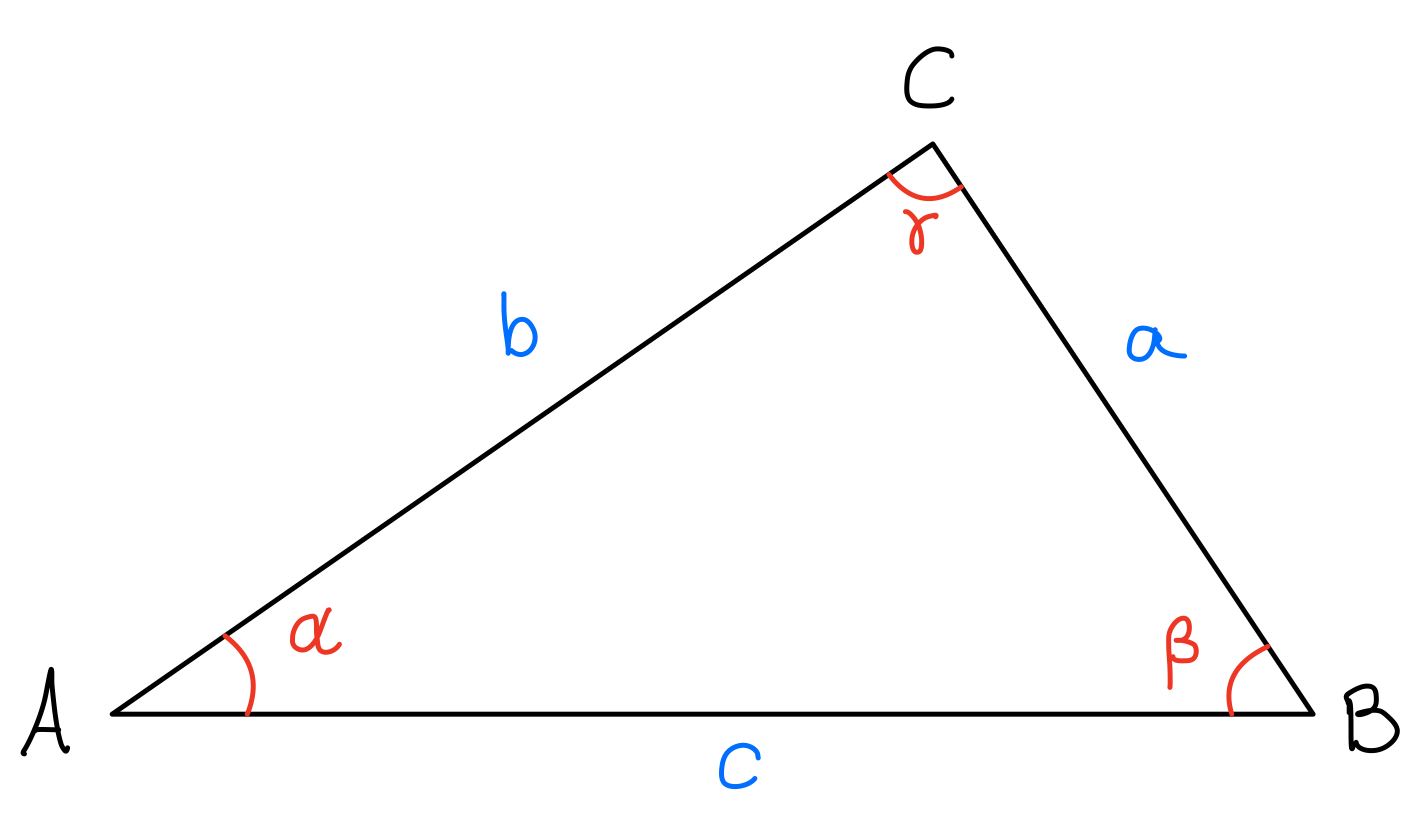
Vi kommer til å bruke cosinusloven til å finne vinkler. Den sier at
\(\begin{align} a^2=b^2+c^2-2\,bc\cos\alpha \end{align}\)
En kjapp forsmak: la A være sentrum av av planeten og B din posisjon. C er posisjonen til den ene satellitten. Dermed vet du avstanden mellom deg og satellitten, hvis du vet de andre verdiene.
Schwarzchild-geometri
Betrakt følgende situasjon: i nærheten av et sterkt tyngdefelt står det en person på et "skall" som omslutter legemet som gir opphav til feltet. Denne observatøren ser på to eventer som skjer nærme han selv. Eventene skjer i hans referansesystem, så han måler egentiden (tiden målt i samme referansesystem som eventene skjer). Langt langt unna befinner det seg en annen observatør. Han befinner seg så langt vekk at rommet rundt han ikke blir bøyd av tyngdefeltet. Dersom langt-vekk-observatøren skal måle avstanden i tiderommet mellom de to eventene som skjer nær tyngdefeltet, må han bruke Scwarzchild-geometri. Det er gitt slik.
\(\begin{align} \Delta s^2=\bigg(1-\frac{2M}{r}\bigg)\Delta t^2-\frac{\Delta r^2}{\Big(1-\frac{2M}{r}\Big)}-r^2\Delta\varphi^2 \end{align}\)
Her er \(M\) massen til legemet, \(r\) radiell avstand fra legemet og \(\varphi\) den tangentielle hastighetskomponenten. Dette resultatet er en av de få analytiske løsningene på Einsteins likning, men det skal vi ikke gå inn på her. Husk at også \(\Delta s^2=\Delta \tau^2\), hvor \(\tau\) er egentiden. Dette resultatet skal vi bruke til å finne forholdet mellom tidsintervallene sendt ut fra satellittene.
Relativistiske enheter
Dere har hørt om Système International d'unitès. Det er kanskje bedre kjent som SI-enheter (Internasjonale enheter). Det er vel og bra, men hva om vi kan måle alt i én enhet? Vi har allerede vært innom hvordan fart er enhetsløs i relativistiske enheter. Hvis vi har en fart i m/s, så deler vi på lysfarten og får en fart uten enhet, som en fraksjon av lysfarten. Dette er svært nyttig, ettersom at lysets hastighet er lik for alle observatører. Vi vet at lengde og tid ikke er det samme, men det vil gjøre utregninger enklere. Vi kan måle masse i meter på følgende måte.
\(\begin{align} M_\text{meter}=\frac{G}{c^2}\cdot M_\text{kg} \end{align}\)
En kjapp enhetsanalyse viser at dette stemmer.
\(\frac{G}{c^2}\cdot M_\text{kg}=\frac{\text{m}^3\text{kg}^{-1}\text{s}^{-2}}{\text{m}^2\text{s}^{-2}}\cdot\text{kg}=\text{m}\)
Dette reiser jo et betimelig spørsmål: hvor mange meter veier jeg? Undertegnede kan avsløre at han veier \(6.17\cdot10^{-26}\,\text{m}\), som tilsvarer \(617\cdot10^{-24}\,\text{m}\), som er \(617\) yoktometer (yokto: kvadrilliondel). Ikke veldig langt, altså.
Gravitasjonelle og relativistiske effekter som feilkilder
Nå er det på tide å starte på selve problemet vårt. Når vi begynner eksperimentet vil klokkene være synkronisert. Dermed vil vi forvente at den aller første målingen vi gjør, så tidlig som mulig etter start, vil være korrekt. Posisjonen vår er
\(\vec{r}=[-1772.491344,-569.529319]\,\text{km}\)
Utover i denne oppgaven kommer vi ikke til å ta med så mange desimaler, bortsett fra der det er helt nødvendig. Verdiene fra den første målingen setter vi inn i en tabell.
| Posisjon (km) | Tid (s) | |
|---|---|---|
| Satellitt 1 | \([1996.089, -4539.368]\) | \(91.5781\) |
| Satellitt 2 | \([3998.348, -2933.164]\) | \(91.5756\) |
| Oss | \([-1772.491,-569.529]\) | \(91.5964\) |
Vi vet at signalet blir sendt med lysfart, så tidsintervallet må tilsvare avstanden fra mottakeren vår til satellittene.
\(\Delta t_1=1.83\cdot10^{-2}\,\text{s}\\ \Delta t_2=2.08\cdot10^{-2}\,\text{s}\)
Tallet 1 vil alltid gjelde satellitt 1 og tallet 2 vil alltid gjelde satellitt 2. Nå må vi prøve å finne ut av hvordan vi kan bruke dette til å anslå vår posisjon. Den åpenbare løsningen vil være å bruke trilaterasjon. Det gjorde vi tidligere da vi ville finne posisjonen vår etter take-off i dette innlegget. Nå skal vi i stedet prøve å bruke vinkler.
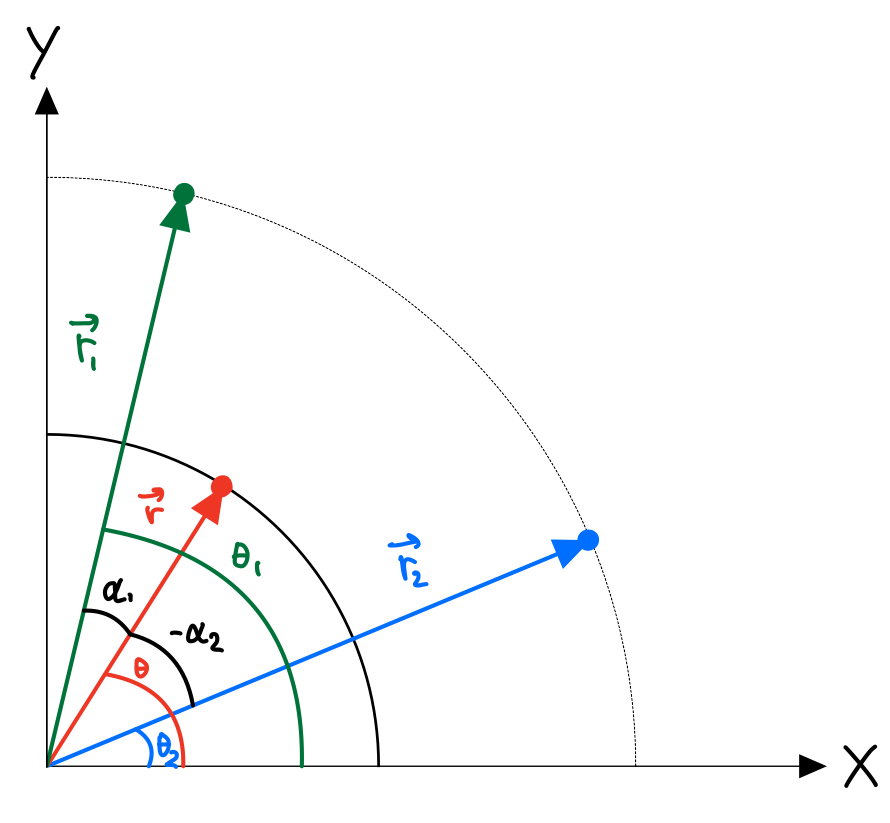
I figuren til høyre har vi forsøkt å tegne et eksempel på hvordan dette kan se ut. Vi har vår posisjon og en vinkel \(\theta\) i positiv omløpsretning fra x-aksen. Det er denne vinkelen vi ønsker å finne. Den grønne og den blå vektoren peker henholdsvis på satellitt 1 og 2, med sine respektive vinkler \(\theta_1\) og \(\theta_2\). Vinklene mellom posisjonsvektoren vår (rød) og de to andre er gitt som \(\alpha_1\) og \(\alpha_2\). Sistnevnte er negativ, siden den går fra den røde vektoren i negativ omløpsretning ned til den blå. Igjen, dette er bare et eksempel og har ingenting med de faktiske verdiene vi har for posisjon. Måten vi skal bruke dette på er at vi vet at avstanden mellom vår posisjon og satellittene er tiden lyset har brukt på å reise til oss. Altså får vi følgende.
\(\begin{align} |\vec{r}_j-\vec{r}|&=c\Delta t_j\\ |\vec{r}_j-\vec{r}|&=\sqrt{(\vec{r}_j-\vec{r})(\vec{r}_j-\vec{r})}=\sqrt{r_j^2-2\,\vec{r}_j\vec{r}+r^2} \end{align}\)
Her indekserer vi med \(j\), for å slippe å gjøre utregningen flere ganger. Merk at \(|\vec{r}|=R\), for vi står jo på planetoverflaten. Ser dere hva som skjer videre? Husker dere hvordan man regner ut prikkproduktet mellom to vektorer? Jo, \(\vec{u}\cdot\vec{v}=|\vec{u}|\cdot|\vec{v}|\cdot\cos\varphi\), hvor \(\varphi\) er vinkelen mellom dem. Dermed får vi dette.
\(\begin{align} |\vec{r}_j-\vec{r}|=\sqrt{r_j^2+R^2-2\,r_jR\cos\alpha_j} \end{align}\)
Det vi altså er ute etter her er vinkelen. Hvis dere ser på figur 2, kan dere se at \(\theta=\theta_j\pm\alpha_j\), avhengig om \(\alpha_j\) er positiv eller negativ. Vi opphøyer i andre og finner vinkelen.
\(\begin{align} |\vec{r}_j-\vec{r}|^2&=(c\Delta t_j)^2\\ r_j^2+R^2-2\,r_jR\cos\alpha_j&=(c\Delta t_j)^2\\ \cos\alpha_j&=\frac{r_j^2+R^2-(c\Delta t_j)^2}{2\,r_jR}\\ \alpha_j&=\pm\arccos\bigg(\frac{r_j^2+R^2-(c\Delta t_j)^2}{2\,r_jR}\bigg) \end{align}\)
Når vi bruker denne formelen på verdiene i tabellen over ser vi at det er en verdi for \(\theta\) som er samsvarende for begge satellittene, \(\theta=-2.83\). Vi bruker polare koordinater
\(\vec{r}=[R\cos\theta,R\sin\theta]\)
og finner posisjonen vår til å være \([-1172.49,-569.53]\,\text{km}\). Dette er som sagt forventet, siden klokkene var synkroniserte ved start.
Nå skal vi ta med de gravitasjonelle og relativistiske effektene. Vi lar nå en langt-vekk-observatør se på situasjonen. Han måler også tiden, med intervall \(\Delta t\), altså uten noen indeks. Vi finner først vår tid, indeksert med tallet 3, relativt til langt-vekk-observatøren.
\(\begin{align} \Delta t_3^2=\bigg(1-\frac{2M}{R}\bigg)\Delta t^2 \end{align}\)
Her er \(\Delta r=0\) og \(\varphi=0\). Vi gjør det samme for satellitt 1 og 2.
\(\begin{align} \Delta t_1^2=\bigg(1-\frac{2M}{r_1}\bigg)\Delta t^2-r_1^2\Delta\varphi_2^2\\ \Delta t_2^2=\bigg(1-\frac{2M}{r_2}\bigg)\Delta t^2-r_2^2\Delta\varphi_2^2 \end{align}\)
Siden \(v_\varphi=r\,dr/dt\), kan vi bruke banefarten fra i stad. Nå kan vi finne tiden satellittene sendte ut posisjonen sin, lest av på vår egen klokke. Vi deler \(\Delta t_3^2\) på \(\Delta t_j^2\) og får følgende uttrykk.
\(\begin{align} \Delta t_3^\text{sat. j}=\sqrt{\frac{1-\frac{2M}{R}}{1-\frac{2M}{r_j}-v_j^2}}\cdot\Delta t_j \end{align}\)
Med dette kan vi finne de nye tidsintervallene våre og se om posisjonen vår endrer seg. De nye intervallene våre ser i første omgang helt like ut som de vi fant i stad, da vi ikke tok hensyn til effektene. Men det er snakk om veldig små endringer. Forskjellen er ikke gjeldende før langt bak komma. Vi kommer derfor ikke til å inkludere verdiene her, men resultatet vårt skal dere få.
| x-komponent | y-komponent | |
|---|---|---|
| Med effekter | \(-1772.48988685\,\text{km}\) | \(-569.53385495\,\text{km}\) |
| Uten effekter | \(-1772.48988692\,\text{km}\) | \(-569.53385473\,\text{km}\) |
| Absolutt feil | \(6.295\cdot10^{-5}\,\text{m}\) | \(2.155\cdot10^{-4}\,\text{m}\) |
| Relativ feil | \(3.907\cdot10^{-11}\) | \(3.784\cdot10^{-10}\) |
| Avstands feil | - | - |
Avstandsfeilen her er så liten at den nesten ikke spiller noen rolle. Men nå skal vi se på hva som skjer når vi lar tiden gå en stund. Igjen, så ser vi at forskjellene i tidsintervallene er vanvittig små, så vi skal kun se på resultatet.
| x-komponent | y-komponent | |
|---|---|---|
| Med effekter | \(-1772.53806085\,\text{km}\) | \(-569.38390719\,\text{km}\) |
| Korrekt posisjon | \(-1772.48988692\,\text{km}\) | \(-569.53385473\,\text{km}\) |
| Absolutt feil | \(48.17\,\text{m}\) | \(149.95\,\text{m}\) |
| Relativ feil | \(2.718\cdot10^{-5}\) | \(2.633\cdot10^{-4}\) |
| Prosentfeil | \(2.718\cdot10^{-3}\,\%\) | \(2.633\cdot10^{-2}\,\%\) |
| Avstand | \(157.50\,\text{m}\) | |
Tiden det har gått mellom disse to målingene er tre timer, 35 minutter og 24 sekunder. Her ser vi tydelig at jo lenger tiden går, jo større vil feilen bli. Hadde ikke GPS-satellittene korrigert for dette kunne de like gjerne ha latt vær å sende de opp. Grunnen til at dette skjer er at klokka går saktere for satellittene, og målingene blir dermed ikke korrekte, ettersom at de anvender radiobølger til å utføre målingene.
Konklusjon
De relativistiske og gravitasjonelle effektene som forekommer mens GPS-satellitter skal beregne posisjoner, spiller svært stor rolle på resultatet. Etter omtrent tre og en halv time har vi regnet ut at feilen er på nesten 160 meter. Dette avviket vil bare vokse og vokse jo lenger tiden går. Selv om det er meget små avvik fra måling til måling, vokser feilen seg større og større.