Vi vil nå se på stjernen vår, og se hva vi kan vite om dets fødsel, livsløp og om den passer inn med de andre stjernene som vi kjenner.
La oss begynne med noe kjent, nemlig Hertzsprung-Russell diagrammet. Hvis du ikke allerede vet er dette en systematisk oversikt over stjernene som kan hjelpe oss med å klassifisere og vite en rekke informasjon om stjernen. Denne informasjonen kan si oss blant annet hvor i livsløpet stjernen er. Hvordan skal vi plassere stjernen vår på Hertzsprung-Russell diagrammet? Jo, la oss se hva aksene er på et vilkårlig diagram.
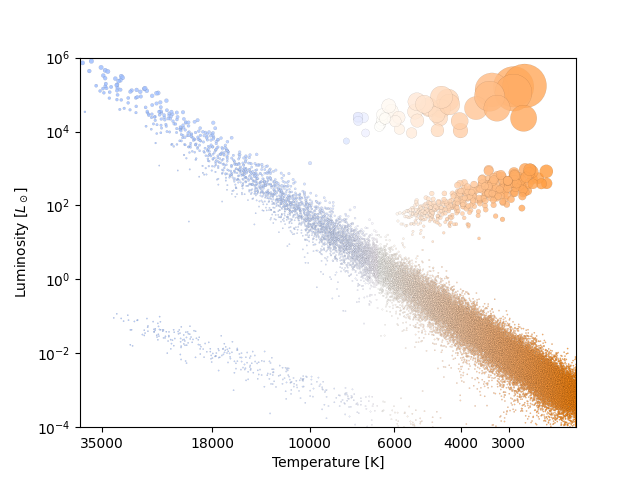
Vi må så vite luminositeten og temperaturen til stjernen. Stjernens temperatur vet vi allerede, som er 11696,4 K, som betyr at den er en stjerne av klasse B. Og har fra Wikipedia at den er så en spesiell stjerne, bare 0,13% av alle stjerner befinner seg her. Vi kan så allerede ha oss en ide hvor stjernen vår ligger.
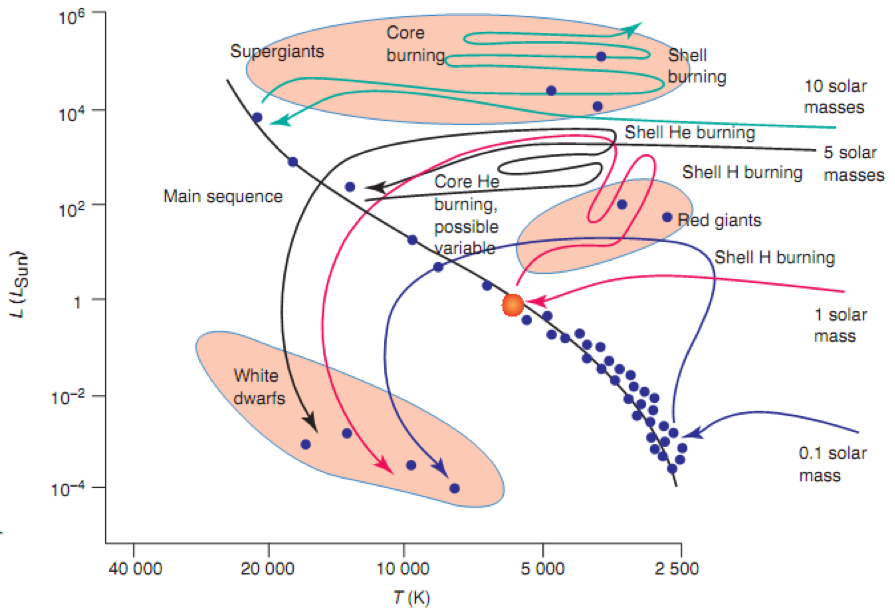
Spørsmålet blir så om den ligger ved de hvite dvergene på den nederste rekken, eller i den store hovedserien som ligger midt i bildet. Gigantene og supergigantene i øvre høyre hjørne er nok ganske usannsynlig, men vi får se på tallene og finne ut hvor stjernen vår hører hjemme.
Hvordan finner vi så luminositeten? Husker du fra en forrige bloggpost hvor vi fant temperaturen på planetene? Jo, vi hadde jo nemlig at luminositeten var oppgitt med fluksen ganget med hele overflaten til stjernen. Fluksen, var jo igjen gitt ved Stefan-Boltzmanns flukslov.
\(F_s = \sigma T_s^4\\ L_s = F_s\cdot A_s \\ L_s = \sigma T_s^4\cdot A_s \\ L_s = 5.3804347\cdot10^{28} \mathrm{W}\)
Vi må så normalisere dette slik at sola (ja, den i solsystemet ditt!) blir 1, akkurat slik vi gjorde med naturlige enheter. Hva var nå solas luminositet? Ah, nemlig, den er \(3.846\cdot10^{26}\). Som gir:
\(L_N = \frac{5.3804347\cdot10^{28}}{3.846\cdot10^{26}} \approx 139.896 \frac{\mathrm{W}}{L_\bigodot} = 1.39 \cdot 10^2 \frac{\mathrm{W}}{L_\bigodot}\)
Vi kan så plotte stjernen vår på HR-diagrammet.
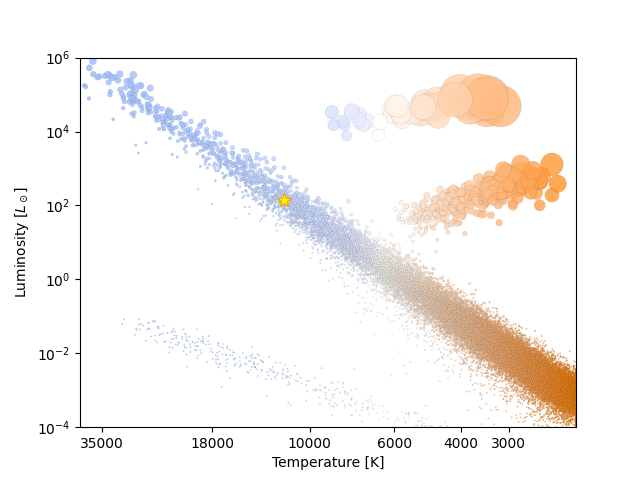
Den ligger så i hovedserien! Dette er hvor de fleste stjerner befinner seg i midten av livsløpet sitt, men... hvor lenge lever egentlig stjernen vår? For å svare på dette resonnerer vi først litt.
Vi vet at en stjerne vil holde seg på hovedserien så lenge den ikke har brukt 10% av hydrogenet i seg. Hva skjer så når 10% av hydrogenet har blitt brukt opp? Stjernen vil begynne å fusjonere heliumet til karbon, dette kommer ut fra den midlere molekylvekten som vi har snakket om i en forrige bloggpost. Den ideelle gassloven sier så at trykket vil synke, og dermed vil den hydrostatiske likevekten ikke gjelde, og må så likestille seg på en ny likevekt (vi snakket mye om dette når vi modellerte atmosfæren). Dette skjer ved at tyngdekraften presser stjernen enda mer kompakt, og det blir varmt nok i kjernen til å fusjonere helium til karbon. Det er så vanskelig å si nøyaktig hvor lang tid en stjerne vil holde seg på hovedserien, men vi kan gjøre noen forenklinger. Vi antar at fra de måtene varme kan transporteres, skjer kun stråling. Dermed kan vi benytte oss av at formelen at 10% av massen blir så energien:
\(E = 0.1mc^2\)
Men vent!! Det er jo ikke sånn at hele hydrogenatomet blir gjort om til energi! Vi må så ha den energien som er dannet per fusjon fra hydrogen til helium. Finner så fram at denne skalaren er 0.7%.
\(E = 0.1mc^2\cdot 0.007\)
Vi husker også at luminositeten er også kjent som effekt, da begge har samme enhet. Vi vet at formelen for effekt er energi over tid, og kan så omskrive uttrykket for å finne tiden. Husker så at vår stjernes masse er \(3.99035 \mathrm{M_\bigodot} \approx 7.9807\cdot10^{30} \mathrm{kg}\).
\(t_{life} = \frac{0.1mc^2\cdot 0.007}{L_s} \approx 9.33175*10^{15}\mathrm{s} = 2.95908\cdot10^8 \mathrm{yr}\)
295 millioner år var ikke så mye da? Sola lever jo i 10 milliarder år, og er 5 milliarder inn i livstiden sin på hovedserien. Dette betyr at stjernen vår forlater hovedserien milliarder av år før solen. Hvordan måles dette opp mot stjerner som er ca. lik i luminositet og temperatur? To stjerner som ligger nære er Sirius og Vega. La oss sette opp en fort tabell over disse:
| Stjernen vår | Sirius (A) | Vega | |
|---|---|---|---|
| Luminositet (\(L_\bigodot\)) | 139.9 | 25.4 | 50 |
| Masse (\(M_\bigodot\)) | 3.99 | 2.063 | 2.135 |
| Temperatur (K) | 11696.4 | 9940 | 9602 |
Tall hentet fra Wikipedia
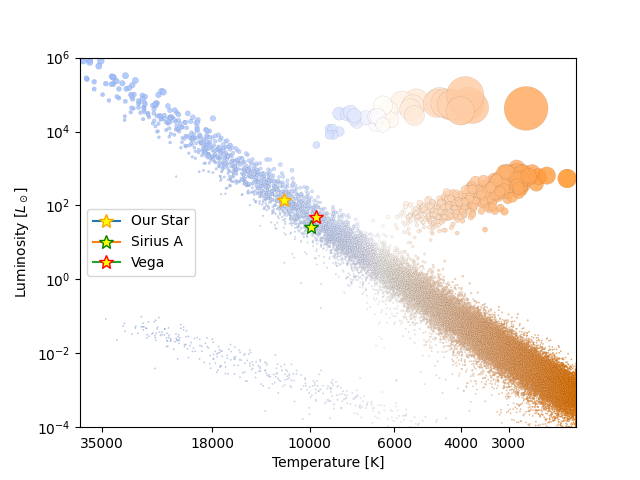
Vi ser at stjernen vår passer godt inn med de andre stjernene. Den er litt varmere, mer massiv som gir den en større luminositet. Ellers virker den til å passe bra. Vi må også huske at Sirius og Vega er begge klasse A stjerner, som ligger under vår. Hva er så levetiden til Sirius og Vega? Jo, fra Wikipedia finner vi igjen at Sirius og Vega har en ca. 1 milliard år på hovedserien. Så stjernen vår dør også raskere enn disse. Siden vi også har en relasjon at livstiden er omvendt proporsjonal med massen i tredje, kan vi godt se at stjernen vår passer inn her.
Nå som vi har snakket om hvor lenge den lever kommer vi jo tilbake til det første spørsmålet; hvordan ble stjernen vår dannet? Vi skal så langt tilbake, til den tid stjernen vår var en gassky flytende i verdensrommet.
Stjernen vår, slik som alle andre stjerner, ble dannet da en gigantisk molekylsky kollapset. Hvor gigantisk var denne molekylskyen? Jo, det er et godt spørsmål, la oss regne på det.
Som alltid, før vi begynner å regne på noe, gjør vi våre antakelser. Vi antar at hele molekylskyen går til stjernen, dette kan vi godt anta da det meste av massen går til stjernen. Bare sola utgjør 99,8% av all massen i sitt solsystem (kilde)! Vi gjør også en antakelse om at molekylskyen var bestående av en uniform gass av 75% hydrogen og 25% helium, og at temperaturen var så frysende kaldt på 10 K. Vi får så en midlere molekylvekt på \(\frac{7}{4}\)u. Hva er det så som bestemmer om at skyen vår skal kollapse? Du kan tenke på dette som når vi prøvde å komme oss i bane rundt destinasjonen vår, at vi måtte være påpasselig at vår kinetiske energi var for høy, ellers ville ikke den potensielle energien fra planeten klare å holde oss igjen! Vi forstår så nemlig at den potensielle energien må være høyere enn den kinetiske. Finner så fra virialteoremet at den kinetiske energien kan maks være halvparten av den potensielle:
\(E_k = -\frac{1}{2}E_p\)
Setter vi dette inn i total energi vet vi så at:
\(E = -\frac{1}{2}E_p + E_p = \frac{1}{2}E_p\)
Så hva blir nå den potensielle energien til hele skyen? Jo vi vet at får hver liten partikkel i den, vil det eksistere en liten del av potensiell energi. Vi husker fra konservative felt at vi kan integrere gravitasjonskraften (og sette et minustegn foran!) for å finne den potensielle energien.
\(\mathrm{d}u = -\frac{GM}{r}\mathrm{d}m\)
Men... hva blir integrasjonsgrensene til m? La oss omskrive litt slik at vi får noe annet. Her kommer antakelsen om en uniform gass, vi kan jo bare tenke på massen som massetettheten ganget med overflaten til et skall med distanse r. Husker du definisjonen av massetetthet?
\(\rho = \frac{m}{V} \\ m = \rho\cdot A\cdot \mathrm{d}r\)
Som gir oss:
\(\mathrm{d}u = -\frac{GM\rho A}{r}\mathrm{d}r\)
Hva er da M? Vi skriver det som lik trykket, ettersom vi antok uniform gass:
\(M = \rho\cdot V\)
Vi får så noe vi kan integrere over når vi faktoriserer ut alle konstantene:
\(E_p = -\frac{16}{3}\pi^2 G\rho^2 \int\limits_0^{R}r^4\: \mathrm{d}r \\ E_p = -\frac{16}{15}\pi^2 G\rho^2R^5 = -\frac{16}{15}\pi^2 G\frac{9M^2}{16\pi^2 R^6}R^5 = -\frac{3GM^2}{5R}\)
La oss nå finne den kinetiske energien. Vi bruker formelen for kinetisk energi til en gass:
\(E_k = NkT = \frac{MkT}{\mu m_H}\)\(E_k = \frac{3}{2}nkT = \frac{3MkT}{2\mu m_H}\)
Vi vet fra viralteoremet at:
\(E_k < \frac{1}{2}|E_p|\)
For at den totale energien skal bli null eller gjøre den potensielle energien dominerende. Vi løser så ulikheten og løser for radien:
\(\frac{3MkT}{2\mu m_H} < \frac{3GM^2}{10R} \\ R < \frac{GM\mu m_H}{5kT} \)
\(R < 2.229\cdot10^{15}\mathrm{m} = 0.2357 \mathrm{ly}\)
Denne radien er også kjent som Jean-radien, radiusen som er minimal for skyen for at den skal kollapse.
Hvor var så stjernen vår på HR-diagrammet før den ble en stjerne? Jo, vi kan jo finne luminositeten på akkurat samme måte som før:
\(L_{GMC}\approx 3.54306 \cdot 10^{28} \mathrm{W} \\ L_{NGMC} = 92.123 \mathrm{L_\bigodot}\)
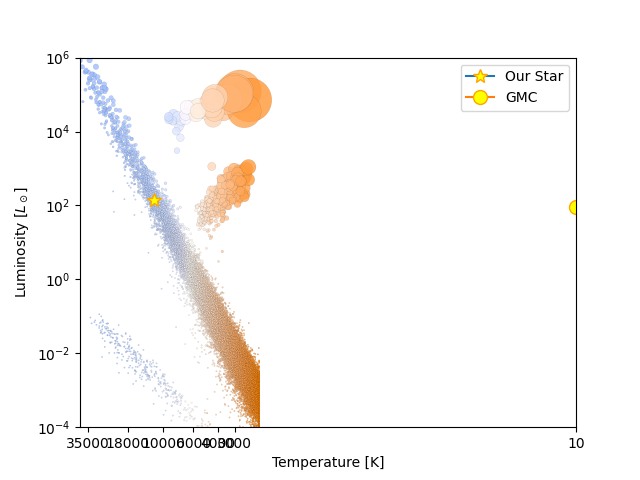
Vi ser så at gasskyen vår er langt langt borte fra hovedserien.
Vi konkluderer så med at vi er så heldig at vi har fått veldig unik stjerne av klasse B. Så har vi funnet hvor lenge den vil oppholde seg i hovedserien, og at den passer godt inn med de andre stjernene. Til slutt studerte vi så noen av minimumskravene for stjernen slik at vi kunne forstå forhistorien dens. Det er likevel mange feilkilder som kan ha oppstått. Vi har gjort ganske mange antakelser for å finne levetiden på stjernen vår. Det å anta konstant temperatur og tetthet, at varmen kun forflytter seg ved stråling, er tall som vil ha en innvirkning på den faktiske levetiden. En gassky kan neppe bli forenklet så mye uten å få en del feil. Den var jo mest sannsynlig ikke unform, besto av en annen fordeling av gasser, var heller ikke en sirkel og heller ikke uniform temperatur. Det er også andre krefter som rotasjon, turbulens og magnetisme som vi så bort ifra. Alle disse har jo så klart en innvirkning på radien og luminositeten vi fant.